PAPER No. 9
Active Disturbance Rejection Control for Web Tension Regulation and Control
2001 IEEE Conference on Decision and Control
Brian Thomas Boulter
Applied Industrial Control Solutions LLC
4597 E Sprague Rd.
Independence, OH, USA 44131
Y. Hou, Z. Gao, F. Jiang ,
Department of Electrical and Computer Engineering
Cleveland State University, Cleveland Ohio, 44115
© ApICS ® LLC 2001
Abstract: A new control method is proposed for tension regulation in a web transport system. It is based on a unique active disturbance rejection control (ADRC) strategy, which actively compensates for dynamic changes in the system, and unpredictable external disturbances. A simulation of an industrial application is used to provide realism. The results show the effectiveness of the proposed tension controller in coping with large dynamic variations commonly seen in web tension applications. The remarkable disturbance rejection capability of an ADRC is also demonstrated.
Tension controls are widely used in web transport and strip processing systems. These systems either feed material from an existing primary processed roll/coil of material into a process for secondary processing, or wind processed material for storage or final shipment. The main purpose of web tension regulation is to maintain the physical integrity of the material that is being processed.
The tension control problem in strip/web processing applications is a complex one because the system dynamics are a function of many process variables that often vary over a wide range. For example, in rolling mills, these variations include changes in roll diameter, product density, web/strip modulus of elasticity, web/strip cross sectional area, the inner speed loop bandwidth and process line-speed. Due to their difficulty and importance in industry, tension problems have drawn the attention of many researchers. One problem is the establishment of a proper mathematical model. Campbell [1] and Brandenburg [2] studied the longitudinal dynamics of a moving web. Campbell developed a mathematical model of a web span but did not consider the tension in the entering span, therefore his model does not predict "tension transfer". This problem was addressed by Brandenburg and Shelton [3], with the assumption that the strain in the web is very small. Brandenburgís work took into consideration the effects of small changes in area that result from strain changes, temperature changes, and register errors.
There are two approaches used in web processing industries for tension control: open-draw control and closed-loop control. In the "draw control" scheme, tension in a web span is controlled in an open-loop fashion by controlling the velocities of the rollers at either end of the web span. W. Wolfermann and D. Schroder [4][5] used an optimal output feedback method to control the speed of the driven rollers. A decentralized observer was designed to decouple the drives from the web tension acting on the driven rollers and this information is used to improve the speed control of the driven rollers. This method leads to considerable improvement in the speed responses of the driven rollers. An inherent drawback of indirectly controlling tension through speed control is its dependency on the open loop relationship between the speed and tension. This control method cannot reject disturbance due to "tension transfer" from adjacent web spans and interaction between adjacent web spans through an intermediate driven roller. Note that tension is also affected by the change in temperature, material, thickness, as well as other operating variables. It is also very sensitive to noise in the speed feedback devices.
The proportional-integral-derivative (PID) control approach is the primary feedback control law used in industry. For tension feedback control, however, because of the significant variations in system dynamics, PID alone has been shown to be inadequate. K. Reid, K. Shin and K. Lin [6][7][8] proposed the fixed-gain and variable-gain PID control of web tension in the winding section. For variable gain PID, the control parameters are continuously updated based on the diameter of the roller, which is a major contributor to the system dynamics. This method uses pole placement techniques.
In this paper, we proposed a new methodology for web tension regulation. It is based on a unique active disturbance rejection control (ADRC) concept. In this approach the disturbances are estimated using an extended state observer (ESO) and compensated in each sampling period. This method was developed by J. Han [9]. A survey paper of this and similar results is available upon request [10]. The proposed ADRC control system consists of the ESO and a nonlinear PD controller. It is designed without an explicit mathematical model of the plant. The controller is designed to be inherently robust against plant variations. Once it is set up for a class of problems within a predetermined range of variation in system variables, no tuning is needed for start up, or to compensate for changes in the system dynamics and disturbance. This method, because of its robustness and disturbance rejection capabilities, is particularly suitable for web tension regulation applications.
In Section II, the web tension problem is introduced. Details of the ADRC control approach is given in Section III. Simulation results based on a simplified linear model and an industrial strip processing application are given in Section IV. Finally, concluding remarks are included in Section V.
II. The Web Tension Regulation Problem
A web refers to any material of continuous flexible strip which is either endless or very long compared to its width, and very wide compared to its thickness. The web has to pass through several processing sections in the manufacturing process of an intermediate or final product. All sections of the continuous process are coupled by the web. Different web tension levels are typically required in each processing section. Severe tension variations in these sections may lead to degradation of product quality, or even the rupture of the material during processing. This results in significant economic loss and negatively impacts process line productivity. In order to minimize the potential for loss, the need arises to adequately control the tension within a predefined range in a moving web processing section.
This research is motivated by the difficult control problem encountered in a web line testing facility, referred as the Lab-line and is shown in Figure 1, at a Cleveland manufacturer. It was used for the purpose of evaluating web handling control strategies. A simplified one-line diagram is shown in Figure 2.
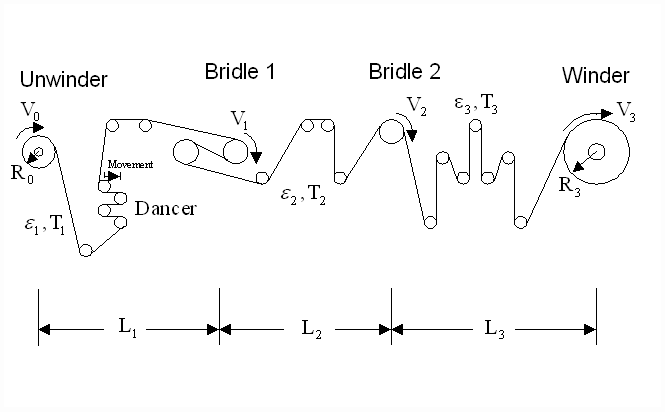
Figure 1. Lab-line illustration
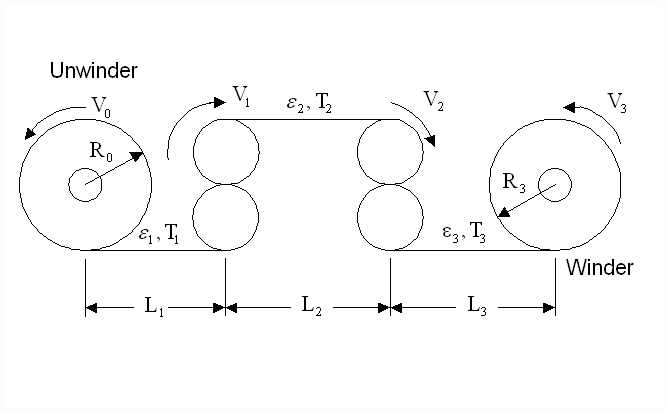
Figure 2. Simplified Lab-line diagram
The tension dynamics associated with the conveyance of web through a single tension zone is described in (1). It is based on the principle of conservation of mass in a mass-flow system [11].
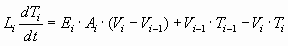 (1) (1)
where:
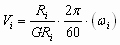 (2) (2)
The motor/load torque equation is:
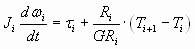 (3) (3)
The above equations can be presented in block diagram format as shown in Figure 3. This modular representation includes the hooks that allow coupling multiple sections together. However, it does not include any damping terms. Note that a rigorous representation of equation (1-3) requires the integrators in Figure 3 to be preset to their respective initial conditions [12].
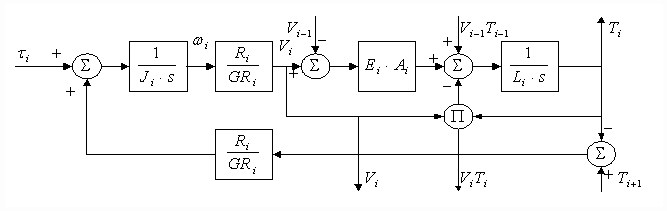
Figure 3 Block Diagram of a Web Tension Zone
For a given operating line velocity LSi, an approximate linear representation of equations (1-3) can be obtained [11]. A block diagram of the linearized model is shown in Figure 4, with the assumptions that 1) the tension in the web entering the tension zone is zero; 2) the system speed reference Vi-1 is constant.
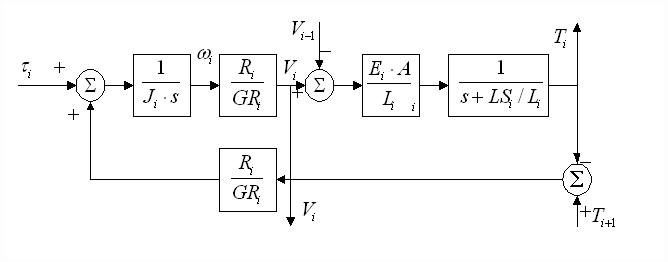
Figure 4 Linearized Block Diagram of a Web Tension Zone
Of particular interest is the behavior of the tension loop at stall (that is when the web stops moving). At this point, with some simplifications, a tension transfer function can be approximated as a typical second order system
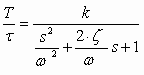 (4) (4)
with 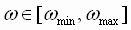 , , 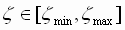 and and 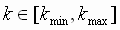 . With a corresponding differential equation of: . With a corresponding differential equation of:
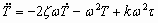 (5) (5)
Considering the tension coupling, dead zone and other nonlinearities in the system as well as external disturbances, a more generic and realistic differential equation for the tension dynamics is
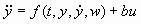 (6) (6)
where y is tension, u is motor torque, and w is the disturbance. Here,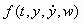 is generally a time-varying nonlinear function that represents the true system dynamics. The difficulties in tension control is mostly due to the fact that the function is generally a time-varying nonlinear function that represents the true system dynamics. The difficulties in tension control is mostly due to the fact that the function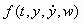 changes significantly during operation and better control strategies are needed to solve this practical problem. changes significantly during operation and better control strategies are needed to solve this practical problem.
III. The Active Disturbance Rejection Controller
The ADRC is based on the idea that in order to formulate a robust control strategy, one should start with the original problem in (6), not its linear approximation in (5). Although the linear model makes it feasible for us to use powerful classical control techniques such as frequency response based analysis and design methods, it also limits our options to linear algorithms and makes us overly dependent on the mathematical model of the plant.
Instead of following the traditional design path of modeling and linearizing 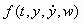 and then designing a linear controller, the ADRC approach seeks to actively compensate for the unknown dynamics and disturbances in the time domain. This is achieved by using an extended state observer (ESO) to estimate y, dy/dt, and and then designing a linear controller, the ADRC approach seeks to actively compensate for the unknown dynamics and disturbances in the time domain. This is achieved by using an extended state observer (ESO) to estimate y, dy/dt, and 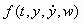 iteratively. Once iteratively. Once 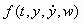 is estimated, the control signal is then used to actively compensate for its effect and reduce (6) to a double integration, which in turn becomes a relatively simple control problem. More details of this novel control concept and associated algorithms can be found in [9,10]. A brief introduction is given below. is estimated, the control signal is then used to actively compensate for its effect and reduce (6) to a double integration, which in turn becomes a relatively simple control problem. More details of this novel control concept and associated algorithms can be found in [9,10]. A brief introduction is given below.
A. The Extended State Observer (ESO)
In order to estimate 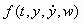 without knowing its analytical form, the plant in (6) is augmented as without knowing its analytical form, the plant in (6) is augmented as
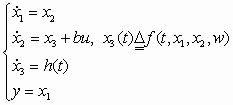 (7) (7)
where h(t) is the derivative of 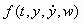 and is unknown. The reason for increasing the order of the plant is to make and is unknown. The reason for increasing the order of the plant is to make 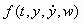 a state set such that a state observer can be used to estimate it. One such observer is given as a state set such that a state observer can be used to estimate it. One such observer is given as
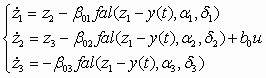 (8) (8)
where b
01,b
02 and b
03 are observer gains, b0 is the normal value of b and fal(∑) is defined as
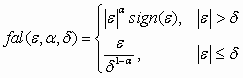 (9) (9)
This observer is denoted as the extended state observer (ESO) and is the corner stone of the ADRC method.
Remarks:
- The nonlinear function in (9) is used to make the observer more efficient. It was selected heuristically based on experimental results. Intuitively, it is a nonlinear gain function where small errors correspond to higher gains. This technique is used widely in industrial applications.
- If ai i=1,2, 3, are chosen as unity, then (8) is equivalent to the well known Luenburger observer found in linear system theory;
- Similar to linear observers, the observer equation (8) reflects our best knowledge of the plant. The information on the range of b in (6) is needed for the selection of b0 in the ESO. If we know more about the plant, such as the roll diameter, which gives us part of
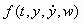 , then this information should be incorporated into the observer to make it more efficient. , then this information should be incorporated into the observer to make it more efficient.
- Note that there is a linear segment in (9) in the neighborhood of the origin. It was discovered experimentally that the nonlinear function in (9) makes the observer converge faster than its linear counter part and the linear section in (9) and makes the output of the observer smoother.
- The proper selection of the gains and functions in (8) are critical to the success of the observer. One way to get started is to design the linear observer first and then gradually increase the nonlinearity to improve the performance. This is particularly helpful for people who experiment with this method for the first time.
B. The Control Law
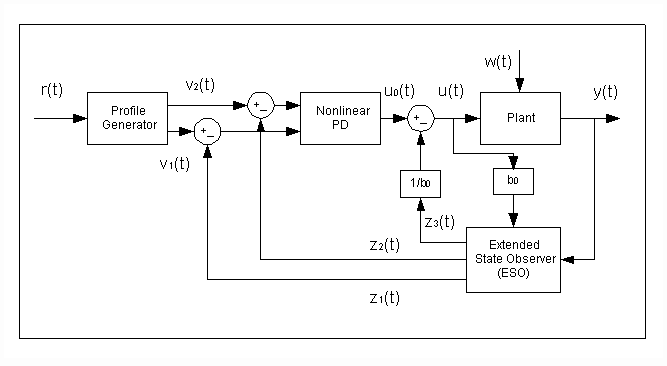
Figure 5. Structure of the ADRC
The architecture of the ADRC is shown in Figure 5. It consists of three components: the Profile Generator which provides the desired transient trajectory for tension to follow from the initial value to the setpoint; the ESO which is described above, and the control law which is defined as
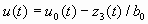 (10) (10)
This control law reduces the plant to a double integration and is controlled by the nonlinear PD controller:
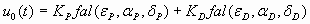 (11) (11)
For example, in positioning applications, e
P = v1 - z1, e
D = v2 - z2, are "position" and "velocity" error, respectively, kP and kD are the gains of the PD controller, and fal(∑) is the nonlinear function defined in (9).
Note that the profile generator generates the desired output trajectory, v1(t), and itís derivative, v2(t). They are then compared to the filtered output, z1(t), and its derivative, z2(t). Clearly, the differentiation of the error is obtained without taking the direct differentiation of the set point or the output. This makes the algorithm much less sensitive to noise in the output and discontinuities in the setpoint r(t).
The critical component here is obviously the ESO. Its parameters need to be tuned properly for the ADRC to work. We find it useful to get a rough linear model from testing data of the real system, based on which the ESO parameters and feedback gains are tuned. It was discovered that once the ESO is properly set up, the performance is quite insensitive to the plant variations and disturbances.
IV. Simulation Study
The Matlab/Simulink package from Mathworks was used for the simulation. The simulation is carried out in two stages. The validity of the ADRC is examined in the first stage using the simple linear model in (5). Once the parameters are well tuned and successful results are obtained, the ADRC is then tested on a simulated industrial web-line in the second stage.
Proof of the concept
The ADRC is first tuned and simulated using the linearized plant in (5) with parameters in the ranges of 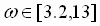 , , 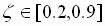 and and 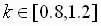 . A discrete version of (8-11) is used with a sampling rate of 1 kHz. For the sake of simplicity the Eulerís formula is used for the discrete approximation. It also shows that this controller should not be sensitive to numeric inaccuracies. . A discrete version of (8-11) is used with a sampling rate of 1 kHz. For the sake of simplicity the Eulerís formula is used for the discrete approximation. It also shows that this controller should not be sensitive to numeric inaccuracies.
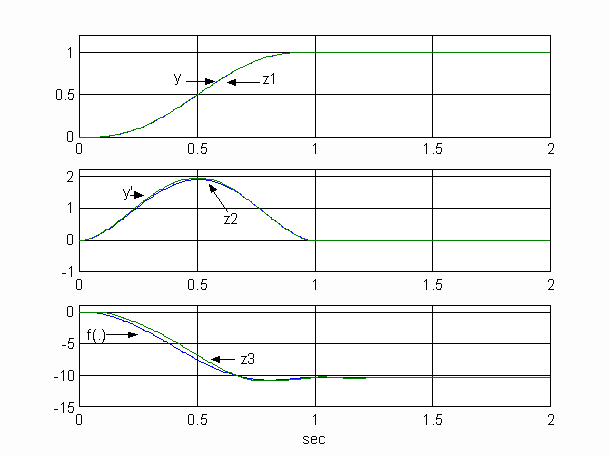
Figure 6 The performance of ESO for simplified model
The ESO output and the plant output are compared in Figure 6. Note that all three outputs of the ESO track their targets quite well. The resulting PD design becomes quite straightforward. The most encouraging part of the simulation is that similar performances are observed for various parameter settings within the range, demonstrating the robustness properties of the controller.
Testing in an industrial setting
Following the successful simulation with the simple model, we then tested the ADRC on a full-scale simulation of the Lab-line shown in Figure 1, which is a four-section process line. The simulation model developed and used by practicing engineers is shown in Figure 7. Note that there are three tension zones but only one tension feedback loop, which is located on the winder side of the process line. The most critical area for tension regulation is at the winder. Note that with the tension loop in place, one may or may not use an inner speed loop on the winder tension regulation scheme. Using the inner speed loop helps to dampen natural frequencies that are lower than the speed loop bandwidth [12]. We elected not to use it for the sake of simplifying the design and also to make the control problem more challenging.
As the web moves through the line, the diameter of the winder roll varies from 3 inches to 24 inches, which roughly corresponds to variations in the linear model of: w from 3.2 to 13, z: from .2 to .9, and k: from .8 to 1.2. Understandably, such changes pose a significant challenge for the controller to be designed for stability, and performance, over the entire operating range.
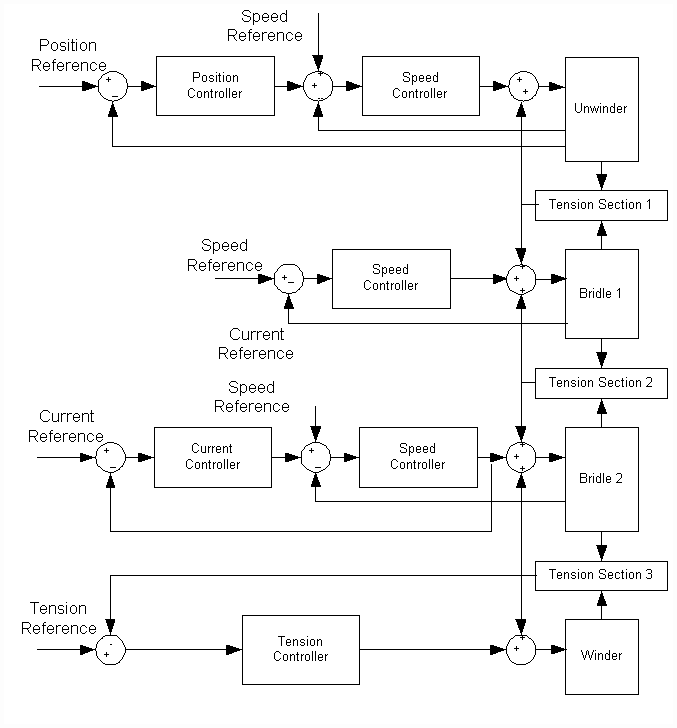
Figure 7 Simulink based industrial simulator diagram
Figure 8 shows the response of web tension loop using the ADRC. The sample period is ts=10ms, which is consistent with many existing industrial tension application hardware capabilities, such as the Rockwell AutoMax DPS UDC Controller. The parameters are fixed for the ADRC while the tests are conducted at different operating conditions, particularly for different winder diameters. The design specifications call for a 1.5 sec settling time and overshoot of less than 10%. The ADRC meets both of these transient requirements for all diameter changes. Two extreme cases are shown in Figure 8. A constant 20% rated torque pulse disturbance is also added at t=5 sec to show disturbance rejection properties. Overall, the results are very encouraging.
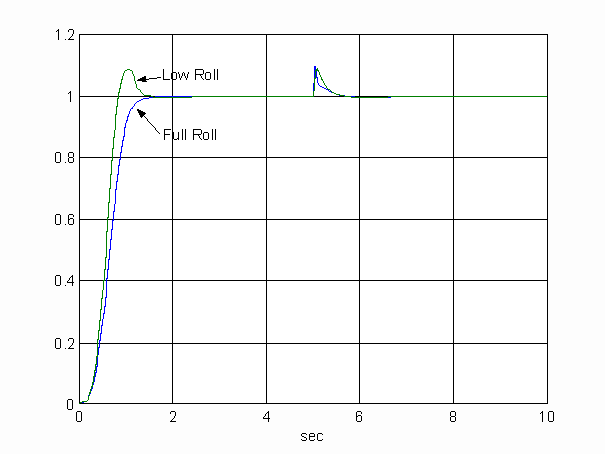
Figure 8. Tension responses at empty and full roll with 20% torque disturbance at t=5sec. (ts=10ms)
Note that there are NO fixed gain controllers that can come close to this performance. Even the variable gain PID controller used in the industrial application did not perform as well in simulation. No direct comparison is made because we believe it was not optimized and the comparison may not be fair.
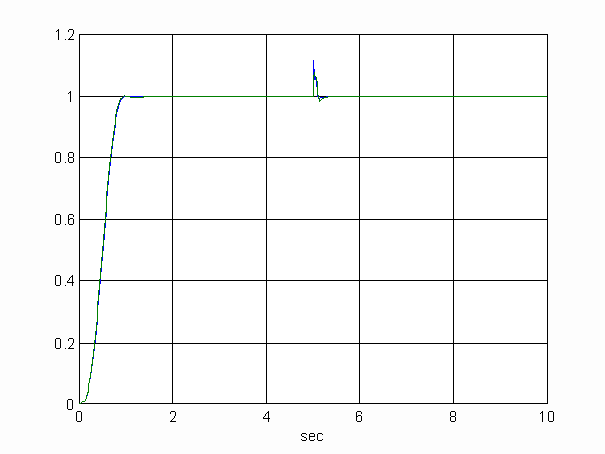
Figure 9 Tension responses at empty and full roll 20% torque disturbance at t=5sec. (ts=1ms)
It was discovered that if a faster sample rate can be used, the ESO can produce a much better estimate, which leads to significantly better results. Figure 9 shows the results of the ADRC, using a ts=1 ms sample period, for the same two extreme operational cases: the empty roll and full roll. The results are astonishing. There is barely any difference between the two responses. With the analog to digital converter running in the range of a microsecond, a 1 millisecond sampling rate will not be an application problem in the near future.
V. Conclusion
A new web tension control method is proposed. The Active Disturbance Rejection Controller (ADRC) is applied to deal with significant dynamic change in the web transport process. The new control algorithm in digital form is simulated on a simulation of an industrial process with very encouraging results. We believe that this is a promising new technology for web applications because 1) itís intuitive; 2) it does not require explicit mathematical models of the plant under control; 3) it is inherently robust. It was shown that once the ADRC controller is setup properly, it can handle a large range of dynamic changes. High sampling rates result in a tremendous improvement in the ADRC control performance.
VI. References
[1] D. P. Cambell, Process Dynamics, Wiley, 1958, pp. 113-156.
[2] G. Brandenburg, "New Mathematical Model For Web Tension and Register Error", Proceedings: 3rd International IFAC Conference On Instrumentation And Automation In The Paper, Rubber and Plastics, Vol. 1, May 1976, pp411-438.
[3] John J. Shelton, "Cause And Effects Of Tension In A Draw-Controlled Web process Line", Proceedings of the First International Conference on Web Handling, Stillwater, Oklahoma, 1991, pp 210-219.
[4] W. Wolfermann and D. Schroeder, "New Decentralized Control In Processing Machines With Continuous Moving Webs", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 96-115.
[5] W. Wolfermann, "Tension Control of Webs Ė A Review of The Problems and Solutions In The Present and Future", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 198-228.
[6] G. E. Young and K. N. Reid, "Lateral and Longitudinal Dynamic Behavior and Control of Moving Webs", Journal of Dynamic Systems, Measurement, and Control, June 1993, Vol. 115, pp 309-317.
[7] Karl N. Reid, Kee-Hyun Shin, and Ku-Chin Lin, "Variable-Gain Control Of Longitudinal Tension In A Web Transport System", AMD-Vol. 149, Web Handling, ASME 1992, pp87-100.
[8] Karl N. Reid and Ku-Chin Lin, "Control Of Longitudinal Tension In Multi-Span Web Transport Systems During Start Up", Proceedings of the Second International Conference on Web Handling, Stillwater, Oklahoma, 1993, pp 77-95.
[9] J.Han, Jingqing Han, "Nonlinear State Error Feedback Control". Control and Decision (Chinese), Vol.10, No.3, Nov., 1994, P221-225.
[10] Z. Gao and Y. Huang, "A New Paradigm for PID Control", submitted for publication.
[11] Brian T. Boulter and Zhiqiang Gao, "A Novel Approach for On-Line Self-Tuning Web Tension Regulation", IEEE Conference on Control Applications Ė Proceedings, 1995, pp. 91-98. IEEE.
[12] Brian T. Boulter, "The Effect of Speed Loop Bandwidths and Line-speed on System Eigenvalues in Multi-Span Web Transport Systems", Proceedings of the 33rd IEEE IAS Conference. New Orleans 1997 .
[13] P. Lin and M. S. Lan, "Effects Of PID Gains For Controller With Dancer Mechanism On Web Tension", Proceedings of the Second International Conference on Web Handling, Stillwater, Oklahoma, 1993, pp 66-76.
[14] K. H. Shin, Karl N. Reid and S. O. Kwon, "Non-Interacting Tension Control In A Multi-Span Web Transport System", ", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 312-325.
[15] K. H. Shin and W. K. Hong, "Real-Time Tension Control In Multi-Stand Rolling System", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 247-262.
[16] B. Walton and B. S. Rice, " Web Longitudinal Dynamics", Proceedings of the Fourth International Conference on Web Handling, Stillwater, Oklahoma, 1997, pp 384-403.
[17] G. E. Young, J. J. Shelton and C. Kardamilas, "Modeling And Control Of Multiple Web Spans Using State Estimation", ASME Journal of Dynamic System, Measurement, and Control, Vol. 111, No. 3, Sept, 1989, pp 505-510.
[18] Pekka Pakarinen, Risto Ryymin, Matti Kurki and Pekka Taskinen, "On The Dynamics Of Web Transfer In An Open Draw", Proceedings of the Second International Conference on Web Handling, Stillwater, Oklahoma, 1993, pp 117-134.
[19] Karl N. Reid and Ku-Chin Lin, "Dynamic Behavior Of Dancer Subsystems In Web Transport Systems", Proceedings of the Second International Conference on Web Handling, Stillwater, Oklahoma, 1993, pp 135-144.
[20] J. P. Ries, "Longitudinal Dynamics Of A Winding Zone", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 264-277.
[21] H. Linna, P. Moilanen, A. Mahonen and M. Parola, "Variation Of The Web Tension At The Roll Change In The Printing Press", Proceedings of the Third International Conference on Web Handling, Stillwater, Oklahoma, 1995, pp 301-310.
Appendix I
Nomenclature
|
Jmotor |
motor inertia [kgm2] |
|
Jload |
reflected roll (load) inertia c |
|
Ji |
Jmotor+Jload [kgm2] |
|
Vi |
iíth roll surface velocity [m/min] |
|
w
i |
iíth motor rotational velocity [rpm] |
|
Ri |
iíth roll radius [m] |
|
GRi |
iíth roll gear ratio |
|
Li |
iíth tension zone length [m] |
|
Ti |
iíth tension zone tension [kgf] |
|
t
i |
iíth roll reflected shaft torque [kgf.m] |
|
E |
modulus of elasticity [kgf/mm2] |
|
A |
cross sectional area [mm2] |
|
LSi |
opearting line speed [m/min] |
|
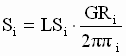 |
iíth motor gear-in speed [rpm] |
|