PAPER No. 10
Applying Drive Specifications to Systems Applications:
Part II: Current/Torque Regulation
2001 IEEE IAS Annual Meeting
Brian Thomas Boulter
Applied Industrial Control Solutions LLC
4597 E Sprague Rd.
Independence, OH, USA 44131
© ApICS ® LLC 2000
Abstract- In web/strip processing lines, a popular control practice is to use torque/current regulators to set web/strip tension. In other applications such as automotive test stands, a fast responsive torque regulator is required. This paper provides guidelines for the useful interpretation of AC/DC torque/current performance specifications in these applications, from a drive systemís application perspective.
I. Introduction
As noted in [3] the technical climate in todayís drive systems business markets has been inundated by drive vendor claims of ever improving drive performance specifications. The objective of this report is to bring those performance specifications that apply to torque/current regulation into technical focus, and provide the reader with a basis for correctly interpreting them from a SYSTEMS /APPLICATIONS perspective. Future papers will address performance issues associated with "cascaded" and "parallel", position and tension regulation schemes. Part I [3] dealt with speed regulation issues.
It is hoped that the reader will walk away from this presentation with the tools required to sift through a given driveís performance specifications, and glean from them those points that are truly of importance to the application in question.
- Paper Overview
The paper is divided into four sections. The first section is composed of this introduction, the second section defines a set of useful terms, the third section defines the most important drive specifications with respect to torque and current regulation, and methods of determining these criteria for a given drive. A set of observations and conclusions are presented in the fourth section
II. Some Useful Definitions
Two definitions that prove useful in understanding a drive system torque/current regulation performance criteria are, control loop bandwidth, and per-normal Inertia.
Control Loop Bandwidth (Fig. 1): Bandwidth is defined as the frequency at which the closed loop response of the controlled variable is attenuated 3 [db] from the set point. It is also approximated as the point at which the open loop gain of the system is unity and is called the "crossover" frequency. The Bode plot graphically represents the magnitude and phase of the ratio of output to input over a range of input frequencies. Therefore, unity gain of the system at the crossover frequency implies that, at that frequency, the output and the input of the open-loop system are equal in magnitude. And at all frequencies below this frequency, the closed loop has unity gain.
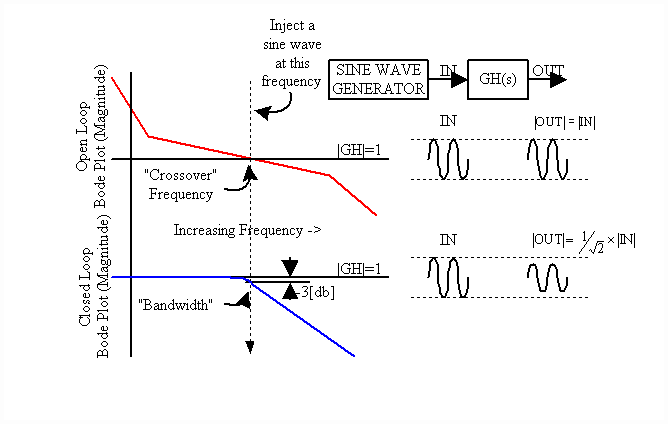
Fig. 1. Bandwidth Definition
Per-Normal Inertia (Fig. 2): Per-normal (PN), or normalized, reflected inertia [sec] is the time in seconds that it takes to accelerate the motor and load inertia from zero speed to motor base speed (Sb) with motor rated torque (tRated) and the given reflected inertia (J).
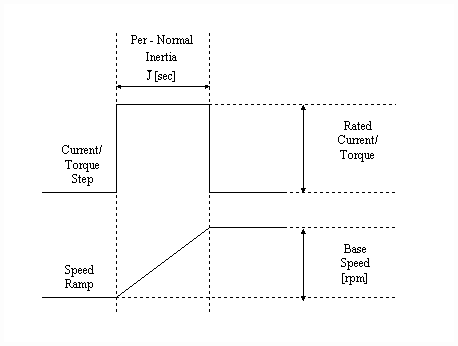
Fig. 2 Per-Normal Inertia [sec]
SI units: 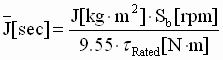 (1) (1)
III. Interpreting Drive Performance Torque/Current Specifications
A. Architecture Description
Current/torque regulators can be implemented as either cascaded or parallel major loops. The cascaded architecture (Fig.3) is implemented with a speed intermediate loop (SML). In this architecture, the current loop (CL) trims the SML which provides a reference to the current/torque minor loop (CML). The parallel architecture (Fig.4) provides a trim for the current/torque major loop directly to the CML, usually through the appropriate SML PI limit. By applying the control signal through the SML PI limit, the drive will not over-speed the motor if a strip or web break occurs during operation. Rather the drive will allow the motor to rotate at the given speed reference plus a small offset that is used to force the SML PI up against the limit.
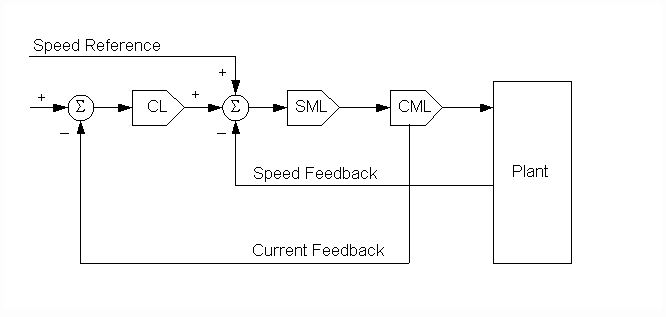
Fig. 3. Cascaded Current/Torque Architecture.
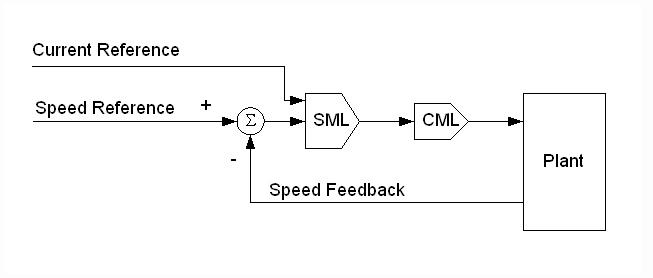
Fig. 4. Parallel Current/Torque Architecture.
These regulation architectures are often used as a way of setting strip/web tension in strip/web processing lines without the need to close a tension loop around a load-cell tension feedback device. They are sometimes called open-loop tension regulators. Specifications that apply to the ability of the drive to set tension in these applications assume that inertia and friction/windage feed-forward compensation have been implemented and calibrated correctly. The tension "error" is then a function of the driveís current/torque linearity and the torque resolution. Following is a description of the feedforward terms.
B. Feedforward terms
Irrespective of the current/torque loop architecture that is used, maintaining a desired web/strip tension during acceleration and deceleration, and over the expected speed range, requires the implementation of feed-forward inertia and friction (loss) compensation. These calculated feed-forward torque terms provide the extra torque needed to accelerate/decelerate the given inertia, and to provide compensation for friction/windage losses. They must be summed in with the current/torque reference that computes the current/torque required to produce the desired web tension.
The per-normal (PN) equation describing the summation of rotational forces at the motor shaft is given as:
|
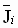
|
PN inertia [sec] |
|
Sb |
motor rated speed [rpm] |
|
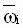
|
PN motor speed (1 = > Sb) |
|
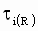
|
rated motor torque [N.m] |
|
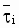
|
PN motor torque (1 = > Rated torque) |
|
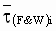
|
PN loss torque (1 => Rated torque) |
|
Ti |
down-stream strip tension [N] |
|
Ti+1 |
up-stream strip tension [N] |
|
Ri |
Roll diameter [m] |
|
GRi |
Gear ratio |
Then:
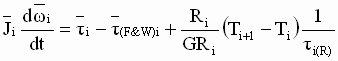 (2) (2)
In terms of motor torque:
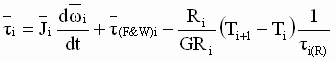 (3) (3)
where:
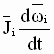 = PN Inertia compensation torque = PN Inertia compensation torque
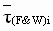 = PN Friction compensation torque = PN Friction compensation torque
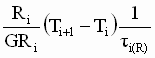 = PN tension drop torque = PN tension drop torque
The torque reference to the drive must include all three of these feed-forward torque terms to maintain a desired tension drop across the driven roll(s), or a desired tension in a winding/unwinding zone, especially while accelerating and decelerating the line.
Note that the friction/windage term is usually measured on-site as a function of line-speed. A lookup table with a pointer that is a function of line speed is then used to generate the friction/windage-loss torque feed-forward reference.
The Inertia compensation term can be calculated based on the known line acceleration rate, and the inertia of the driven roll. If the roll diameter changes (such as in a winder) the inertia can be calculated based on the known material density, and the measured roll diameter and width.
C. Drive Linearity and Tension Error
Assuming that the on-site commissioning engineer has set-up feed-forward inertia and friction/windage-loss terms perfectly, then the current/torque regulatorís ability to maintain a desired strip tension over the entire application operating range will depend on the linearity of the torque/current loop. A given driveís specifications that refer to linearity should be converted to strip tension deviations DT using the following equation:
SI Units: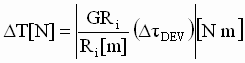 (4) (4)
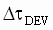 is the drive specified maximum torque deviation as a function of speed, temperature, and current/torque reference obtained from specifications provided by the drive vendor. Most drive vendors are reluctant to give out this detailed information, but it will be shown that this data is of far more interest than generic speed and torque step response data in torque sensitive applications. The following example illuminates this concept. is the drive specified maximum torque deviation as a function of speed, temperature, and current/torque reference obtained from specifications provided by the drive vendor. Most drive vendors are reluctant to give out this detailed information, but it will be shown that this data is of far more interest than generic speed and torque step response data in torque sensitive applications. The following example illuminates this concept.
Example 1 AC Drive Ė Winder Application
In Fig. 5 a not-to-scale, family of curves that describe the mapping between measured and command reference torques over the speed range of a generic winder AC drive and matching motor is presented. This drive/motor combination exhibits poor torque mapping characteristics. These poor mapping characteristics may result from non-linearities in the flux algorithm over the speed range, and from non-linearities in the vector algorithm over the torque range. Such non-linearities may result from mismatching between the motor and drive, an inferior motor, or poorly engineered vector and flux algorithms. This type of data is obtained from a dynamometer test stand, with a fixed speed regulated drive opposing a torque regulated drive. Torque feedback is taken from a torque load cell in the coupling.
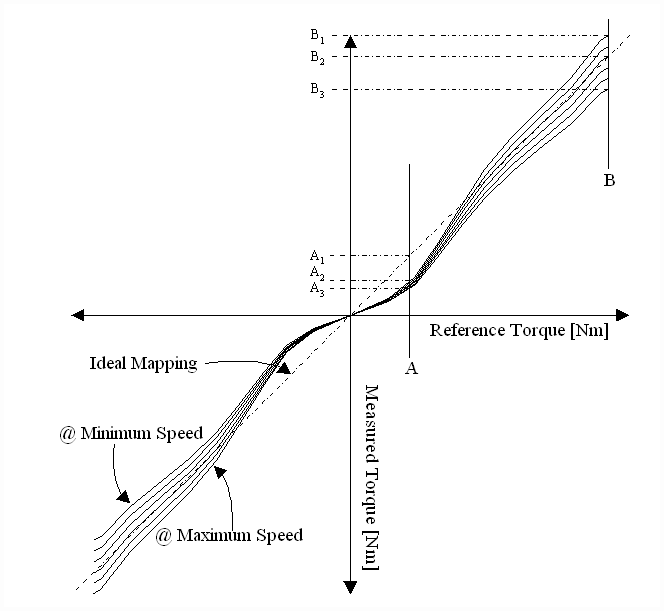
Fig. 5 Sample Winder Drive Torque Response (not to scale)
|
A (Ref) |
A1 |
A2 |
A3 |
|
1 [Nm] |
1 [Nm] |
0.85 [Nm] |
0.75 [Nm] |
|
B (Ref) |
B1 |
B2 |
B3 |
|
10 [Nm] |
10.1 [Nm] |
10 [Nm] |
9.8 [Nm] |
Let us assume that, in this example, the winder must be designed to maintain tension within +/- 2.5 % of set-point over the operating speed and torque range. Further let us assume that the material is extremely sensitive to tension deviations from set-point, and will either break or deform with too little or too much tension. Let:
|
RMIN |
0.1 [m] Min. Roll Dia. |
|
RMAX |
1 [m] Max. Roll Dia. |
|
GR |
1 Gear ratio |
|
TREF |
10 [N] Tension set-point |
|
t MIN |
10*0.1 [Nm] Torque Ref @ Min. Roll Dia. |
|
t MAX |
10*1 [Nm] Torque Ref @ Max. Roll Dia |
At empty core the set-point tension of 10 [N] requires a 1 [Nm] torque reference, we see from Fig. 5 that the actual torque may vary from 0.85 to 0.75 [Nm], therefore the actual tension will vary from 8.5 to 7.5 [N] over the speed range. At full roll the actual torque may vary from 9.8 to 10.1 [N], therefore the actual tension may vary from 9.8 to 10.1 [N] over the speed range. From (4) and the prescribed tension deviation specification we obtain the following:
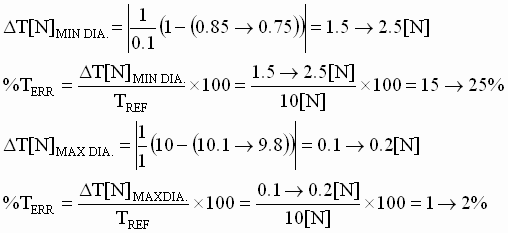
It is clear from the above example that the non-linearities in the AC torque regulator result in out-of-specification tension at the roll core. The drive vendor may state that the drive is operating within specification because the deviation is within 2.5% of the "rated" tension of the drive. [N]. Where "rated" tension is defined as the maximum tension possible at empty core, or in this case 100 [N], however that is of little comfort while attempting to wind a roll from core and encountering strip/web breaks, while rolling bad material.
E. Static Accuracy (Resolution):
The static accuracy of a torque or current regulator is a function of the discretization in the minor loop algorithm. This in turn is usually a function of the number of counts used for the current/torque reference, or the DACís and ADCís used in the regulator, whichever produces the lower limit. In some drives, DACís are not used, instead a look-up table or counter is used. The effective resolution in these applications will be equal to the number of bits used in the counter or look-up table.
Few, if any, analog DC current regulators are used in systems applications today. There are still numerous analog AC torque loops, however there is always a D/A - A/D converter pair in the control loop interface to the digital drive controller. For these reasons, the discretization of the torque reference and feedback will still provide the guidelines for estimating torque resolution in both AC and DC drives.
In the majority of drives available for systems applications, the resolution of the ADCís and DACís is chosen to be commensurate with the accuracy of the current/voltage measuring devices used in the drive. Making this assumption, Table 1 can be used to determine the static accuracy of the minor loop algorithm. Note that, when the DACís and ADCís are of the same resolution, the first or second least significant bits are dropped due to internal conversion noise, errors in the measuring devices, and internal computation error.
If the drive vendor designed the drive to be cost effective, you can be fairly certain that the ADCís and DACís used are the least expensive for the drive technology used. With this in mind the drive dependant resolution of the minor loop reference will almost always reflect the A/D and D/A technology used in the minor loop. This is not always true; for example, a drive may be implemented with 16 bit A/Dís and 16 bit counters, however, because of legacy issues, the effective resolution of the CML reference may only be 1 part in 4096 counts. It could have been as high as 1 part in 32K if the design was optimal. With this in mind, the last limiting factor in current/torque resolution is the resolution of the current/torque reference.
Table 1.
|
Ref (Counts) |
ADC |
DAC |
Resolution |
|
4096 |
8 bits |
8 bits |
+/- 1 part in 64 128 128 |
|
4096 |
10 bits |
8 bits |
+/- 1 part in 256 |
|
4096 |
10 bits |
10 bits |
+/- 1 part in 256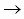 512 512 |
|
4096 |
12 bits |
10 bits |
+/- 1 part in 1K |
|
4096 |
12 bits |
12 bits |
+/- 1 part in 1K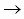 2K 2K |
|
4096 |
14 bits |
12 bits |
+/- 1 part in 4K |
|
4096 |
14 bits |
14 bits |
+/- 1 part in 4K |
|
4096 |
16 bits |
14 bits |
+/- 1 part in 4K |
|
4096 |
16 bits |
16 bits |
+/- 1 part in 4K |
|
> 4096 |
14 bits |
14 bits |
* +/- 1 part in 4K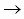 8K 8K |
|
> 4096 |
16 bits |
14 bits |
* +/- 1 part in 16K |
|
> 4096 |
16 bits |
16 bits |
* +/- 1 part in 16K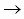 32K 32K |
|
> 4096 |
20 bits |
16 bits |
* +/- 1 part in 64K |
|
> 4096 |
20 bits |
20 bits |
* +/- 1 part in 262 524K 524K |
* Note: for floating point (FP) current/torque minor loop algorithms with a FP reference, the effective resolution will equal the indicated maximum possible range. For discrete current/torque minor loop algorithms, the effective resolution will equal the lower of either the reference resolution or the indicated range.
To convert the tabulated resolutions to strip/web tensions the following procedure can be used:
Step 1: Determine the effective resolution of the current/torque algorithm (Table 1)
Step 2: Determine the tension resolution with Eq. 5 below
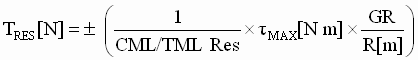 (5) (5)
Example 1, Current Regulated DC Film Machine Turret Winder: (English Units)
|
Output Counter: |
16 bit :Firing Angle resolution |
|
ADC: |
16 bit :Current/Voltage ADC resolution |
|
CML Ref : |
10000 :CML Reference [counts] |
|
HP: |
300 :Motor power [HP] |
|
GR: |
1 :Gear Ratio |
|
Rmin: |
0.5 :Empty Core diameter [ft] |
|
Rmax: |
3 :Full Roll diameter [ft] |
|
Sb: |
1750 :Motor base speed [rpm] |
Step 1: CMLRES = 1 part in 10,000 (limited by the CML reference resolution)
Step 2: tMAX = 300 * 5250 / 1750 = 900 [lb ft]
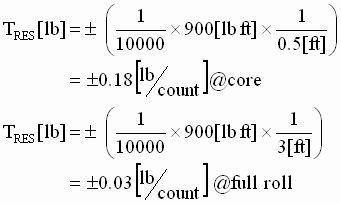
F. Comparison between AC and DC Drives
As shown in the above examples, drive torque linearity and torque resolution are important specifications that must be considered when evaluating and selecting a drive for a given application. However, as a general rule, how do DC and AC drives compare with respect to torque linearity?
In general, AC vector drive technology is not as mature, or as straightforward to implement as DC drive technology. DC drives are typically more linear over their entire operating range. This is especially true when we consider field-weakening applications. The relationship between field strength and torque is well understood and easily linearized in DC applications. The same is not true in AC applications. It behooves the user of an AC drive that incorporates a flux-weakening algorithm to obtain sufficient data on the linearity of the drive/motor combination over the application operating range to ensure that, in torque critical applications, the application specifications will be met.
A further consideration that needs to be made is with respect to AC vector temperature compensation algorithms. Not all temperature compensation algorithms are created equal. If this may be an issue (i.e. operation in extreme temperature ranges), a family of curves shown in Fig. 5 for the expected range of temperatures should be obtained.
In the authorís experience, many field service engineers solve the application problems associated with the above non-linearities in the AC torque algorithm by "fudging" friction compensation look-up tables and/or implementing a linearizing look-up table that utilizes torque reference as a pointer. This is possible if tension or torque feedback is available from a feedback load-cell used only for monitoring purposes. If a load cell is not available, the start-up engineer is "flying blind" and, unless experience shows him that the problem is in the vector/flux algorithms, he/she will have difficulty solving the problem. For example to solve problems with winding at empty core, he/she may increase the tension set-point, only to find that the web/strip breaks or deforms at full roll.
Ignoring the non-linearities of the vector and flux algorithms, it should be pointed out that the effectiveness of this approach to setting strip/web tension is only as good as the start-up engineerís ability to set up the inertia and friction/windage loss compensation schemes. This becomes especially noticeable during line accelerations and decelerations. In addition, the friction/windage loss values are time varying, so the calibration of the pseudo-tension regulator will drift over time. If the application is a tension critical one, such as the above example, it will require re-calibration on a scheduled basis.
It should also be noted that this architecture will not compensate for any load disturbances that occur in a given process. Any specifications that deal with setting tension using current/torque regulators, cannot specify dynamic tension regulation performance, only static tension specifications can be specified. However, static and dynamic performance specifications for current/torque regulation can be specified. To put this statement into perspective consider the following example:
A customer installs a DC parallel current regulator on an aluminium foil coating machine entry-section un-winder. After start-up the customer complains about entry section strip breaks that occur with great regularity when a set of nip-rolls nips the thin material. He points at the drive and states that "the unwind regulator is not regulating tension properly". The on-site service engineer points at the feedback display and states that "we are regulating torque perfectly", and indeed the estimated torque feedback is a flat line. It is clear that it is impossible for the process dependant tension disturbance attributed to the nip rolls biting the web, to be compensated by an open loop tension regulator. Unfortunately, in this application, the problem is not the current regulator on the unwinder, but rather the source of the disturbance in the process itself. The parallel current regulator by itself will not be able to solve this customer problem because it is an open-loop tension regulator.
G. Cascaded Current/Torque Loops
Cascaded current/torque regulators (Fig.1) have much lower bandwidths than parallel regulators. This is because they are cascaded with a speed loop that has a significantly lower bandwidth than the current/torque minor loop. Although this disadvantage can easily be remedied by feeding forward the current/torque reference and summing it with the CML reference.
When to use a cascaded current loop?
Despite the lower bandwidths associated with these loops, they do have several distinct advantages that make them attractive in some applications. The most important of these is the ability of the speed loop to dampen system natural frequencies [1], [2], [5].
A good rule of thumb states that, if the speed loop bandwidth is greater than the dominant (lowest) natural frequency of the system, a cascaded regulator can be tuned to dampen process/machine induced web/strip tension disturbances. If the system natural frequencies are higher than the speed loop bandwidths, the cascaded architecture will not provide any significant benefits. It is usually not worth the effort of including an active speed loop in the system design. A parallel (Fig. 2) architecture, with a passive speed loop, should be used. This is especially true with respect to winders/unwinders.
H. Cascaded current/torque loop dynamic accuracy (Bandwidth):
As stated previously, the dynamic accuracy of a cascaded current/torque major loop will only reflect the ability of that loop to regulate current or torque, not tension.
For systems with natural frequencies greater than the bandwidth of the speed intermediate loop, the bandwidth of cascaded current/torque regulators should be tuned to equal 4/3rds the bandwidth of the speed regulator with which it is cascaded. Therefore:
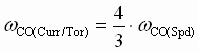 (6) (6)
A detailed description of cascaded current/torque regulator tuning can be found in [2]. Speed loop tuning is described in [3], [4], [5]. In some applications, such as winders, the speed loop bandwidth may vary with buildup, while the current/torque major loop bandwidth is required to remain constant. In these applications, the load shock recovery time of the cascaded major loop will vary with the speed loop bandwidth, despite having a constant current/torque major loop bandwidth. This is described in the following section.
 (7) (7)
In order to take advantage of the damping provided by the speed loop [1], [2], [5], in systems where the speed intermediate loop bandwidth is greater than the dominant natural frequency of the system, a different current/torque major loop tuning approach is taken. In these applications the response of the current major loop is very poor, but the damping of the dominant system natural frequency is very good. Because the application of this tuning approach does not address current/torque performance issues, but rather damping of natural frequency issues, it will not be considered in the following discussion.
I. Cascaded Current/Torque Loop Load Shock Recovery Time:
A useful measure of cascaded current/torque loop performance is load shock recovery time. This is the time it takes the cascaded current loop to return to a given percentage of maximum current/torque feedback, after a load shock equivalent to a given percentage of rated current/torque is applied to the current/torque minor loop reference. This specification is strictly a method for specifying performance, and providing an understanding of the expected cascaded current/torque-loop command reference tracking, it should never occur in an application.
This specification can be expressed in terms of the ratio of speed loop bandwidth to current/torque major loop bandwidth, as shown in Fig.6. A family of curves is presented showing the effect of the ratio of speed loop bandwidth to current torque major loop bandwidth, on the current/torque recovery time. The curves are for ratios of Speed Loop Bandwidths to Current/Torque Loop Bandwidths of 1:1 to 1:10,with 5 logarithmically spaced steps.
NOTE: Fig. 6 applies ONLY to cascaded current regulators WITHOUT web/strip coupled to the drive (i.e. locked rotor test).
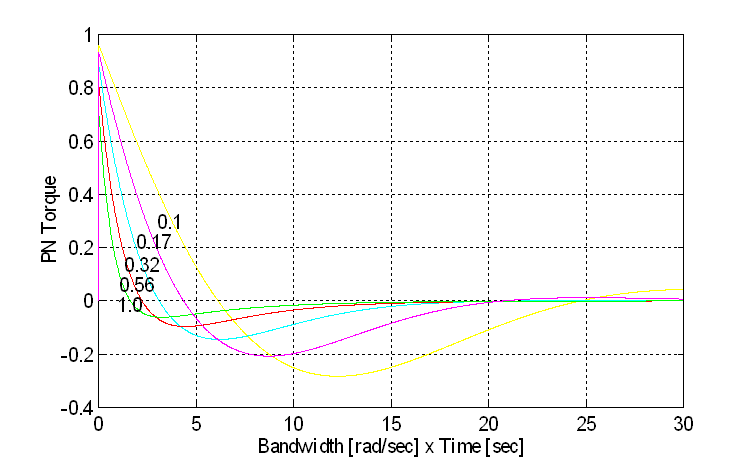
Fig. 6 Cascaded Current/Torque Loop Load Shock Recovery Time
The following procedure can be used, with Fig. 6 to calculate the time to recover to a current/torque of 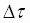 after a after a 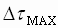 current/torque deviation caused by an X% load shock: current/torque deviation caused by an X% load shock:
Let: tR = Rated motor torque
Step 1: Determine the bandwidth of the Current/Torque loop
(BWLOOP).
Step 2: Determine the maximum current/torque deviation
(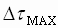 ) for the specified load shock ) for the specified load shock
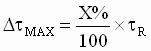 (8) (8)
Step 3: Determine the Time to recover from the load shock:
- Let
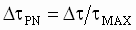 , Where Dt is the desired recovery torque. , Where Dt is the desired recovery torque.
- Calculate the Y-Axis lookup value using Eq. 16
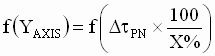 (9) (9)
- Calculate the time it takes to recover using Eq. 17
 (10) (10)
It should be emphasized that this is a worst case scenario. This is because a torque step shock (injected at the torque reference to the CML, and recovered from by the Cascaded torque/current loop) will never occur in an actual application.
J. Parallel Current/Torque Loops
Parallel current/torque regulator bandwidths are equivalent to the bandwidth of the current/torque minor loop. The static performance is described in the same way as the cascaded curent/torque regulator.
Parallel current/torque loop dynamic accuracy (Bandwidth):
The dynamic accuracy of a parallel current/torque major loop, like that of the cascaded current regulator, will only reflect the ability of that loop to regulate current or torque, not tension, in the presence of typical machine/process induced load disturbances. In fact there will be no damping of system natural frequencies when this architecture is deployed.
As stated above, the bandwidth of parallel current/torque regulators that are implemented with correctly tuned current/torque minor loops is equal to the bandwidth of the CML. The drive specifications that apply to the CML response, can be used to define the current/torque performance of the parallel current regulator.
K. Torque response specifications
In certain applications, such as automotive test stands, machine tooling equipment, or cut-to-length machines, the response of the torque/current regulator is critical. To qualify a particular drive for these applications, the drive vendor may supply specifications that apply to a torque step response, or they may specify bandwidth.
Some vendors prefer to specify a step response, arguing that the CML step response is 2nd order and that the 3 [db] definition of bandwidth does not apply. Depending on the CML control algorithms the step response of a given torque/current regulator may be either 1st or 2nd order. It is in the procurerís best interest to request plots of locked rotor current/torque step responses from the drive vendor for the purpose of identifying the response as 1st or 2nd order. If there is no overshoot, 1st order criteria can be used, if there is overshoot 2nd order criteria can be used.
To enable the reader to compare apples to apples when comparing torque/current response specifications, the following criteria are provided.
Torque/current loop response criteria:
First order
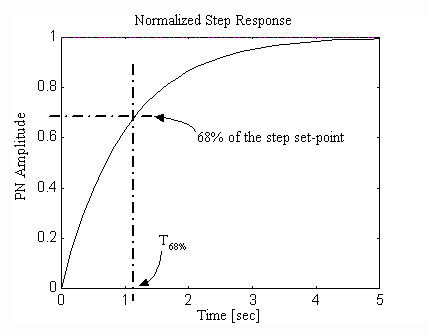
Fig. 7 First order step response
The relationship between the step response of a 1st order system (Fig. 7) and the bandwidth is given as:
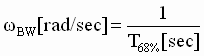 (10) (10)
Where T68% is the time it takes for the step response to reach 68% of set-point.
Example 1. 1st order MG set current step response
A locked rotor current step of an MG set produced no overshoot, and the time to 68% of set-point was measured to be 30 [msec]. The Bandwidth of the CML is 1/0.03 = 33 [rad/sec]
Second order
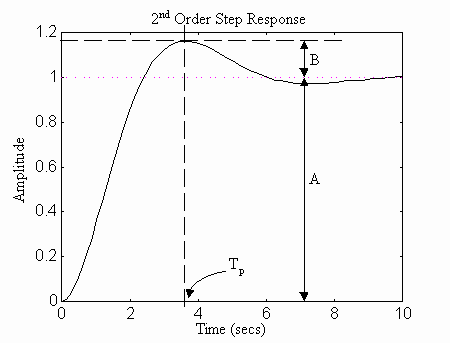
Fig. 8 Second order step response
The relationship between the step response of a 2nd order system (Fig. 8) and the bandwidth is given as:
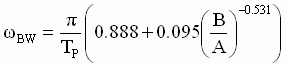 (11) (11)
Where TP is the time it takes for the step response to reach its peak, A is the step set-point, and B is the amount of overshoot.
For evaluation of 2nd order system responses, it is not correct to use the T68% measure from the first order systems criteria. This incorrectly skews the bandwidth when overshoot is excessive. The bandwidth measures provided above are the best method that can be used to compare 1st and 2nd order system responses. It provides an approximation of the crossover of both 1st and 2nd order systems that is roughly equivalent. In second order systems the crossover measure is slightly lower than the 3 [db] closed loop frequency, and can be approximated as the frequency at which the phase is shifted 90o.
The problem with estimating AC vector drive torque step responses is that the torque feedback is itself estimated in the vector algorithm. If a load cell is used to obtain this data the transient dynamics of the load-cell and coupling will corrupt the results.
Assuming the torque estimate is not reliable and the step response cannot be used, a closed loop steady-state sinusoidal test as described in the section describing bandwidth can be used. To assess the bandwidths of AC drives a high performance load-cell is required. The load-cell and associated signal conditioning equipment should have a bandwidth that is at least 10 times higher than the expected bandwidth of the drive. The 2nd order system bandwidth can then be estimated as the frequency at which the closed loop feedback (taken from the load-cell in a dynamometer test bed) is shifted 90o-95o from the reference.
Example 2. 2nd order AC Vector torque step response
Assume the estimated torque step response is reasonably good, producing a second order response with a time to peak of 1.15 [msec] and a 20% overshoot. The Estimated bandwidth is
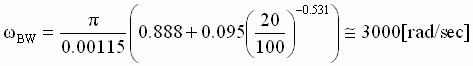
IV. Observations and Conclusions
From the discussion in the previous sections it is clear that, for applications where regulating the torque level is critical, care should be taken to ensure that the AC or DC drive/motor combination is selected to meet the system performance requirements using the described methods. In particular, the drive linearity over the operating range, and the torque resolution should be verified as sufficient for the given application. In applications where the torque response is critical, and the torque level is not an issue, the bandwidth or step response data of the AC or DC torque loop should be used as a guide.
References
[1] B. T. Boulter, "The Effect of Speed Loop Bandwidths on System Natural Frequencies in Multi-Zone Strip Processing Lines" , Transactions of the IEEE-IAS, pp. 126 - 134 Jan/Feb. 1999,
[2] B. T. Boulter, " Improving Bridle Low-Speed Regulation Using Cascaded Current Followers ", Transactions of the IEEE-IAS, pp. TBD, Jul/Aug 2001,
[3] B. T. Boulter, " Applying Drive Performance Specifications to Systems Applications Ė Part I, Speed Performance ", Transactions of the IEEE-IAS, pp. TBD, Jul/Aug 2001,
[4] B. T. Boulter, J. M. Haboustak, "Theory of Operation of the Auto-Calibrated Center Winder Speed Loop and Position Major Loop", S.E.R. 195, Rockwell Automation Internal Engineering Document, pp. 1 - 101, 04/20/96.
[5] Wolferman, W., "Tension Control of Webs", Proceedings of the 3rd International Web Handling Conference, Oklahoma State University, Stillwater OK, pp. 198 - 226, June 1995.
|