PAPER No. 4 SUMMARY
The Effect of Speed Loop Bandwidths and Line-speed on System Natural Frequencies in Multi-Span Strip Processing Systems
1997 IEEE IAS Annual Meeting
Brian Thomas Boulter
Applied Industrial Control Solutions LLC
4597 E Sprague Rd.
Independence, OH, USA 44131
© ApICS ® LLC 2000
Abstract - Web Handling and Strip Processing systems (SPSís) are composed of multiple tension zones. These zones are separated by driven rolls such as bridles whose speed is regulated by a closed loop controller. Given that the typical tension regulator regulates tension by trimming the reference to a closed speed loop controller, the designer of the tension regulator cannot ignore the effects of closing the speed loop, and line speed, on the strip processing system natural frequencies. These natural frequencies are typically computed as the eigenvalues of an equivalent translational cascaded spring-mass system. This paper discusses these effects.
I. INTRODUCTION
Most frequency domain analysis of strip processing systems (SPS's) involves obtaining the transfer functions from an input variable of interest to an output variable of interest. The most common transfer functions used in this type of analysis are those that provide the analyst with spectral information about system variables that directly affect product quality, such as strip strain (or tension) and roller velocity. For example, the transfer function from shaft torque to tension feedback, or from shaft torque to speed feedback are of interest to both the control system engineer and the O.E.M. The control system engineer is interested in these transfer functions because he is responsible for designing the speed and tension regulators and these variables are controlled through the shaft torque produced by the motor. The O.E.M., because he is interested in ensuring the control system vendor satisfies performance guarantees on speed and tension regulation that directly affect the quality of the final product.
System eigenvalues (or natural frequencies) are defined as the roots of the characteristic polynomial of a system of linear time-invariant (LTI) differential equations. In a linear analysis of the SPS the denominator of all SPS transfer functions will be composed of poles whose location in the s-plane are equivalent to the system eigenvalues. Often the analyst assumes the SPS can be modeled analogous to a mass-spring system where the roll inertias (Ji) and the strip springs (Ei*Ai /Li) are analogous with the translational masses (Mi) and springs (ki). The transfer functions from torque (ti) to speed (wi) and tension (Tj) are assumed to be analogous to the transfer functions from a disturbance force (fi) acting on the mass (Mi) to the translational speed of the mass (Vi) and the force in the spring {ki(xi-xi-1)}. This approach does not lump the closed speed loop regulators into the plant model. In a more practical sense, the eigenvalues resulting from such an analysis can be defined as the poles of the transfer function from any motor torque ti to any tension feedback Tj, or speed feedback wi, in a SPS where all the speed regulators are operating open loop.
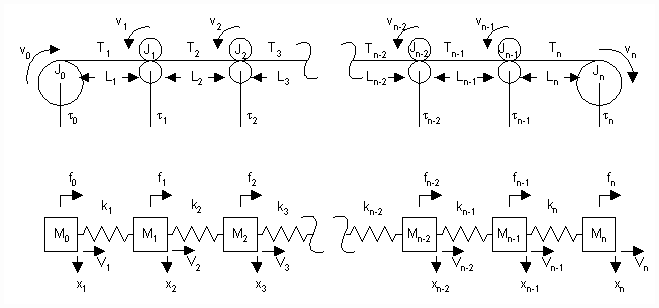
Figure 1. A Typical Mass-Spring SPS Representation
Figure 1 shows the rotational system and the equivalent mass-spring translational system from which the eigenvalues of such an analysis are typically obtained. It is composed of an entry section fed by a winder that unwinds unprocessed strip, a process section where proprietary strip processing is performed, and a delivery section that winds the processed strip into rolls.
Figure 2. Is a single line diagram of a typical SPS including the drives and speed loops. The entire system may be divided into 'n' tension zones that are separated by 'n+1' driven rolls. The unwinder (payoff reel), winder (tension reel) and driven rolls (bridles, calenders etc.) are in turn driven by a power source (Current/Torque Minor Loop - CMLi). The reference to the CMLi is proportional to a desired torque (ti) and comes from a speed regulator (a PI regulator - SPIi) that regulates speed to match a desired speed reference wri.
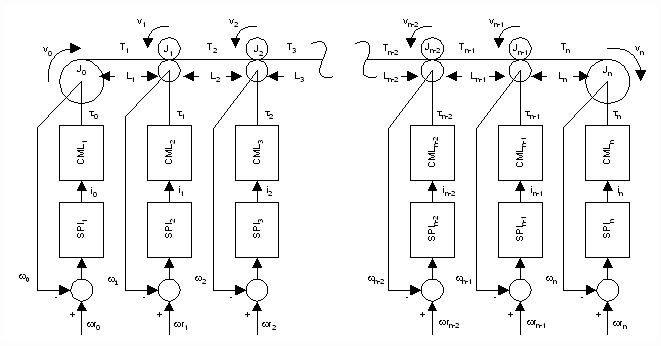
Figure 2. A Typical SPS Including Drives and Speed Loops.
Given that tension regulation in strip processing systems is performed by an outer tension major loop that cascades into a speed minor loop, the eigenvalues of SPSís that are obtained without the inclusion of the closed speed loops are not useful to the control system engineer responsible for the design of SPS tension regulators. Rather, the design of a single-input, single-output (SISO) tension regulator for the 'ith' section in Figure 2. will require an approximation of the transfer function from the speed reference (wri) to the tension feedback (Ti or Ti+1). This transfer function, which includes the closed speed loop, represents the plant the tension regulator is controlling. The tension regulator may use the tension feedback Ti (i.e. drawing material to control the tension in the 'ith' section) or Ti+1 (feeding material to control tension in the 'i+1' section) to regulate the tension around a desired setpoint.
There are exceptions to the cascaded architecture. Specifically, in winders, a direct reference to the CML from either a tension or current regulator may be used. However for the sake of brevity only the cascaded architecture will be discussed in this paper.
Obtaining a transfer function from wri to Ti is a fairly simple task if there are only two masses and one strip section (e.g. an unwinder and a winder directly coupled by the strip). Approximate transfer functions for this application are derived in [1], [2]. However the coupling of additional sections into the system makes the derivation of an analytically exact transfer function unwieldy and, as sections are added, beyond the capabilities of even the most sophisticated symbolic math programs.
While the approach taken in this paper is one based on linear system theory, the author avoided presenting cumbersome sets of transfer functions and their derivations. This was done with the knowledge that, in the analysis of an actual strip process application, there exists a profusion of non-linear contributions that render exact linear transfer functions more or less inaccurate, depending on the application. The approach taken in this paper is one that describes the expected behavior of the transfer functions in terms of the effect of speed loop bandwidths, and line speed, on the system eigenvalues. The expected behavior is expressed as a series of observations phrased in terms of closed speed loop bandwidths, line speed time constants, and natural frequencies.
III. CONCLUSIONS
It is clear from the above discussion that the designer of cascaded tension regulators for multi-span strip processing systems should consider the effect of the speed loop bandwidths on the s-plane location of the SPS eigenvalues when designing tension regulators. Based on the above discussion several conclusions can be drawn:
A. The higher the bandwidth of the SPS speed regulators the greater the damping of problematic SPS natural frequencies.
B. If possible, the O.E.M. process design team should strive to create symmetric systems (similar Wiís in all the sections and per-normal inertias that are approximately equal). This enables consistent damping of SPS eigenvalues with section speed regulators that have identical bandwidths.
C. The per-normal inertias (and by implication the motor horsepowers) and the torsional stiffness of the drive shafts should be selected such that the speed regulators can be tuned for wCOís that will provide adequate damping of the expected SPS eigenvalues. This significantly improves the performance of the tension regulators.
D. O.E.M.ís should be aware that compensation as a function of line speed may be required in tension loops as line speeds increase and the span lengths decrease.
E. If an LTI linear system analysis is used to determine the SPS eigenvalues it can be considered a worst case analysis if the eigenvalues are computed to determine the minimum bandwidth of the speed regulators required to satisfy Observation 2.b. The actual eigenvalues of the system will always be less than or equal to these analytically derived values.
A. Tuning The Tension Regulator
As a note of interest, the tuning of a tension regulator for a SPS with speed loop bandwidths that satisfy Observation 2.b for all the product that is processed through the system becomes a fairly simple task. The lead and lag frequencies of a lead/lag compensator and a PI regulator lead are tuned as shown below:
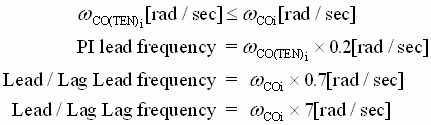
Briefly, the PI lead frequency of the PI controller should be set to 1/5 the desired tension loop crossover. The tension loop crossover should be less than or equal to the speed loop crossover. The lead/lag lead frequency is set to approximately cancel the damped pole from the plant at 0.7 times the speed loop crossover. Recall that the pole at 0.35 times the speed loop crossover is approximately canceled by the transmission zero from the speed PI regulator (i.e. the speed loop PI lead frequency). The lag of the lead/lag compensator is then placed at 10 times the lead/lag lead frequency to ensure that only a minimum of phase margin is lost in the tension regulator. The gain can then be adjusted on-site so that the step response of each tension regulator satisfies a time to peak measure that reflects the desired tension loop bandwidth. Equation (13) can be used to make this determination.
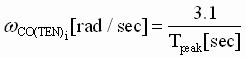 (13) (13)

|