© ApICS ® LLC 2000

A self-tuning control scheme is proposed for tension regulation in a web handling system. A matrix interpolation based computationally efficient self-tuning method is first described. The frequency domain model of the plant is then derived. Simulations of the on-line tuning are presented and a comparison is made with current tension regulation methods. The paper closes with a discussion of cognizant implementation issues.

Web tension regulators are typically implemented with a PI controller as shown in Figure 4. The PI parameters must be tuned to provide a stable and satisfactorily responsive system for the entire spectrum of web material processed through the tension regulated section of the process. In processes where there is a large range in web cross-sectional areas this tuning approach results in a closed loop system that is less than optimally tuned for most of the web material processed through the system and optimally tuned for only a small range of web material. At the time the line is being commissioned the usual tuning approach is to process product with the maximum available and minimum available cross-sectional areas. The regulator proportional and integral gains are empirically adjusted so that acceptable tension regulation is realized. A service engineer remains on-site to observe the behavior of the system during normal production runs. Should any instability be encountered during this "baby-sitting" period re-tuning (or "tweaking" as it is affectionately called) is conducted to ensure that the system will be handed over to the customer in a tuned state that minimizes down-time during normal production runs.

While it is highly desirable to analytically derive an algorithm for pre-tuning the PI regulator parameters based on customer supplied web and plant parameters, unknowns such as web damping, friction, and roll slippage make the derivation of such an algorithm difficult. The usual approach is to heuristically tune the PI controller on-site as described previously. Should instability occur when web material with extreme cross-sectional areas is processed through the system the need arises to re-tune the loop. A better approach would be to provide a self-tuning regulation scheme that obviates the need for empirically finding a single unique set of stable tuning parameters for the entire range of products processed through the system.

To this point in time adaptive and/or self-tuning regulation schemes have not been considered for web handling systems. This fact can be attributed to the complexity of the existing time-domain algorithms, and the associated hardware and software implementation difficulties. K. J. Astrom in [12,13 and 16] and I. D. Landau in [17] summarize a variety of self-tuning regulation approaches using PID and feedback/feedforward techniques. In general most of these approaches are computationally complex. Knowledge based systems have been implemented utilizing fuzzy logic and other rule based approaches with some success [19, 20, 21]. These approaches require customized rules based on the given application, and are not practical for systems that are required to be tuned "out-of-the-box" with minimal customization. Recent developments in the field of self-tuning control have led to some exploration of frequency domain loop shaping self-tuning algorithms. These algorithms are based on iterative procedures that minimize a cost function [1,5 and 10]. With the exception of the rule-based algorithms, the algorithms used in the above adaptive and/or self-tuning regulation schemes do not lend themselves well to a-priori computation of the time required to converge to a solution. In general, the above self-tuning techniques are not computationally efficient enough, nor is the algorithm execution time predictable enough, to be used in self-tuning regulation (STR) for web transport systems. Distributed Control Systems (DCS), today’s standard industrial control platform, are implemented with constrained computational resources requiring efficient algorithms with predictable execution times.

The STR method proposed in this paper is neither complex nor difficult to implement. It identifies controller parameters through an interpolation algorithm that utilizes a desired open loop frequency response and frequency domain information from the plant. The core of the algorithm is expressed in finding the least squares solution of a system of linear equations. It is, therefore, extremely efficient and predictable. For these reasons this particular STR algorithm is attractive for self-tuning implementations in a DSP based DCS platform. The self-tuning algorithm is extensible and can be extended to any SISO control scheme.

To introduce the reader to the proposed STR algorithm and this particular implementation, the self-tuning algorithm is derived in Section 2. A web transport plant is described in Section 3. together with its associated mathematical model. The simulation results of both a typical web tension regulator and the proposed regulator are presented in Section 4. To clarify the benefits of on-line tuning based on a measured plant frequency response as opposed to of-line tuning based on the frequency response of an analytically derived transfer function, Section 4 presents a comparison of the these two approaches. A discussion of implementation considerations can be found in Section 5.

IMPLEMENTATION ISSUES

The object of good tension regulation in a web transport system is to produce good product. In the metals and film/plastics industries any excessive deviation in tension typically results in product that must be scrapped. Since the stimulus required to obtain a meaningful plant frequency response with an FFT will, in these industries, result in material that must be scrapped it follows that self-tuning be performed seldom and generate a minimum of waste material (Quite often, in these industries, a process’s profit margin is tightly linked to the amount of scrap material produced in a given time period ). For these industries the application of the described STR requires some thought and planning. If it is possible to excite the web in a stall condition, waste can be minimized. Applications in the metals industries that would meet this criteria, include rolling mills and tension levelers.

Rolling mills are employed in the metals industries to reduce the thickness of a web of metal and at the same time achieve a significant increase in hardness. This is accomplished by a combination of squeeze force acting on the web through a pair of extremely hard work rolls, and the stretching of the web with tension regulators either side of the work rolls. STR tuning could easily be accomplished at stall, after threading, but before the web is ramped up to line speed. The length of web in a typical reversing mill is only about 20 - 30 [ft]. Rolling mill operations typically scrap threaded material so there would be no increase in scrap material using the STR algorithm for tuning in this application.

In the metals industries, web that has been annealed in a furnace is pock-marked with surface deformities that are the direct result of the annealing process. A tension leveler is used to apply controlled strain at the web surface to effectively remove the deformations. The input and output of the leveler are speed regulated bridles (the "drag" and "drive" bridles) operating with slight differences in speed reference. The regulators either side of the "drag" and "drive" speed regulated bridles are tension regulated to minimize tension disturbances inside the leveler. This configuration, like the rolling mills described previously, may also be tuned with the STR algorithm at stall, after threading, but before ramping the process line to line speed. Waste would be minimized.

It would not be practical to initiate the STR algorithm for tuning tension regulators in the furnace sections of continuous annealing lines. Continuous annealing lines, as implied by their name, run continuously. A welding and/or web stitching machine is used to create a continuous web from many different product coils. These lines are only stopped when a breakdown occurs or when maintenance must be performed. Knowing that about 30 [sec] of data is required to obtain a meaningful FFT of the plant and that annealing lines operate at running speeds around 600 [ft/min], approximately 300 [ft] of material will have to be scrapped. For lines that run a wide range of products with relatively short lengths (in the range of thousands of feet) a substantial reduction in profitability due to scrap will be realized if the STR algorithm is employed.

Some industries process web where product quality is not sensitive to tension deviations. In these industries good tension regulation is required to minimize tear and product bunching on speed regulated process drive rolls. At low line speeds bunching and tearing is not problematic. Typically the need for faster line speeds has provided the impetus for tension regulation. The paper industry is a good example. In these industries the STR algorithm could easily be employed to tune up tension regulators in continuous process lines if the line speed is reduced during the tuning algorithm’s execution. No waste of material would occur.

Mill management systems provide a medium through which controller configurations for particular set-ups may be stored. Using such a management system would alleviate the need for initiating self-tuning for previously run product set-ups. In addition the self tuning algorithm need not be initiated for every product set-up, but rather for those where there is a significant change in product parameters or a predetermined error measure is exceeded.

The step stimulus used in the simulation may not be practical for most systems. For example, materials such as steel do not stretch much and a very little change in speed results in a significant change in tension. For these systems significantly smaller random speed steps would be required. If the system is employed without a speed minor loop, the step stimulus may be applied directly to the current reference and the resulting FFT would not include the speed loop. The use of a speed intermediate loop has been the subject of much controversy in web handling systems. Some industries, such as film and plastics, demand it. In other industries, such as steel and paper the split between the two tension regulation approaches is about 50-50. One of the objectives of Section 2 was to provide an understanding of what effect the inclusion of a speed intermediate loop has on tension regulation. This effect was summarized in the concluding remarks of Section 2.

Should the situation arise where a regulation scheme must be devised for a system where the plant dynamics are not well known, Anstaklis and Gao [2] describe an algorithm whereby the order of the controller can be determined iteratively based on a user defined set of constraints. This method would be very useful for the development of a generic STR compensator and could easily be litmus tested with a simulation similar to that presented in this paper. It would be interesting to compare regulation with STR tuned regulators using regulator structures obtained using the algorithm described in [2] with STR tuned regulators of lesser and greater order.

This paper did not investigate the use of frequency weighting in 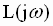which is also discussed in [2] and [3]. Use of this technique may prove useful in reducing the number of points required in the pseudoinverse. For any implementation in hardware a reduction in the number of points used in the pseudoinverse will result in a reduction in computation time. This is extremely desirable in large systems where computational resources are constrained and emphasis is on ever increasing sample rates. In addition, the time taken to find the least squares solution to the system of linear equations of a particular application can be identified. Once identified system computational resources may be allocated in a predictable manner.

In conclusion, the evident elegance and straightforward implementation of the STR algorithm presented in this paper shows great promise for its application in contemporary industrial control engineering practice. It is in no way limited to the tension problem presented, but may be applied to any of a number of SISO control applications.

Figure 1. Proposed STR Scheme

Figure 2. The Physical Plant

Figure 3. The Plant Block Diagram (Including Web-Damping and Viscous Friction)

Figure 4. A Typical Non STR Web Tension Regulation Scheme As Used In Industry Today

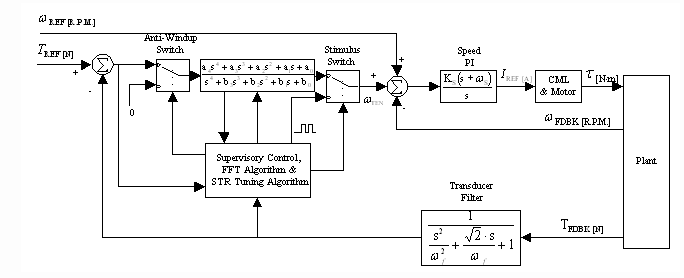
Figure 5. Proposed STR Regulation Scheme (As Implemented In Simulation)

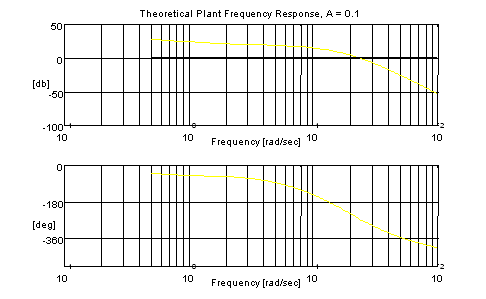
Figure 6. Theoretical Freq. Resp. (A = 0.1 [cm^2])

Figure 7. Estimated Freq. Resp. (A = 0.1 [cm^2])

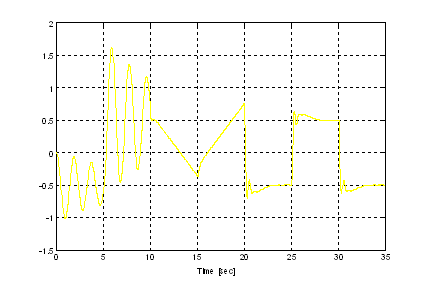
Figure 8. STR Tuning (A = 0.1 [cm^2])

Figure 9. Theoretical v’s On-Line Tuning (A = 0.1 [cm^2])

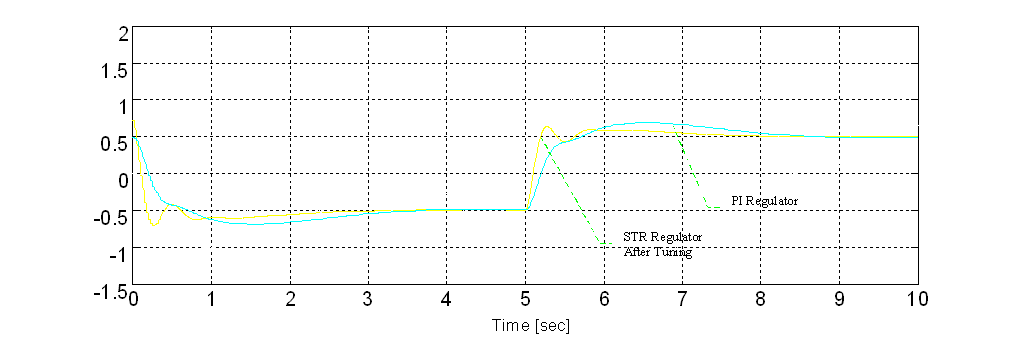
Figure 10. Comparison of PI Regulation and STR Regulation (A = 0.1 [cm^2])

Table 1. Simulation Set-up Parameters