APPLIED INDUSTRIAL CONTROL SOLUTIONS
ApICS LLC.
Winder Dancer Control
and
Analysis of Dancer Oscillations
B. T. BOULTER
© ApICS ® LLC 2000
INTRODUCTION
A winder position loop is typically implemented in a cascaded fashion with a speed minor loop (SML). The two loops cannot be tuned independently of each other. The tuning of the position loop is entirely dependent on the tuning of the SML. For example, if the bandwidth of a given SML can be determined at any point in the build-up of a roll, a feedback lead/lag filteer can be tuned to obviate the effective lag that is roughly equivalent to the bandwidth of the SML and thereby provide adequate phase margin in the position loop at its crossover frequency. It is phase margin that guarantees stability in any control system design. If the bandwidth of the speed loop is not consistent over the build-up of a roll the tuning of the lead/lag in the position feedback must adapt as a function of the speed loop bandwidth or instability may result.
It should be noted that any system configuration where a minimum operational speed loop bandwidth is equal to or greater than 2 times the fixed position loop bandwidth a lead/lag filter in the feedback is not needed, adequate phase margin can be obtained using only a position loop PI regulator. Given this, it is logical to assume that, for any given dancer system, an attempt should be made to obtain the highest possible speed loop bandwidth, and thereby simplify the position loop regulator tuning.
The two most important factors limiting the bandwidth of the speed regulator are the per-normal inertia ( [sec]) of the driven system and torque jitter limitations. Per-normal inertia can be expressed as the time it takes to accelerate the driven system, measured at the motor shaft, from stop to motor base speed with rated motor current. Per-normal inertia is the single most important quantity that must be identified in order to tune a speed loop. Torque jitter is a phenomena that arises from having too much gain in the speed loop. It is easily recognized as a violent excitation or vibration felt at the motor shaft. This is independent of torsional resonance phenomena but it has been known to excite torsional problems as well. To better explain an implementation of the above regulation schemes, two control strategy descriptions follow: [sec]) of the driven system and torque jitter limitations. Per-normal inertia can be expressed as the time it takes to accelerate the driven system, measured at the motor shaft, from stop to motor base speed with rated motor current. Per-normal inertia is the single most important quantity that must be identified in order to tune a speed loop. Torque jitter is a phenomena that arises from having too much gain in the speed loop. It is easily recognized as a violent excitation or vibration felt at the motor shaft. This is independent of torsional resonance phenomena but it has been known to excite torsional problems as well. To better explain an implementation of the above regulation schemes, two control strategy descriptions follow:
A description of ApICS LLC adaptive speed loop tuning algorithm for winders. This algorithm is implemented in such a way as to maximize speed loop bandwidth over build-up while ensuring that torque jitter (a phenomena that can destroy the mechanics of the driven system) is kept at reasonable levels. In addition a system identification test that identifies system inertia and friction at empty core, and also computes the inertia of the roll at any given diameter, is implemented in this adaptive scheme. Experience has shown that this approach results in a significant improvement in system performance over the entire build-up of the coil. A description of the ApICS LLC adaptive position loop for winders. This algorithm is implemented in concert with the adaptive SML. The bandwidth (or crossover) of the SML is calculated and used to adapt the tuning of the winder dancer position loop. The algorithm is also implemented with a set of tuning variables that greatly simplify the tuning of the position loop while guaranteeing stability over the entire range of roll inertias. There are two variables, the first allows for adjustment of the position loop crossover frequency and the second allows for adjustment of the position loop damping. The regulation scheme currently in place does not have this algorithm implemented.
Before presenting the two control strategies, the nomenclature used in the report is introduced. Following the description of the two regulation schemes a linear analysis of the system is presented. This analysis presents as is, and as proposed, system bode plots and step responses for the full range of expected diameters and roll inertias. A brief discussion is also included to cover the relationship (or lack there-off) of current/torque loop bandwidth and dancer position regulation. This is to address an expressed concern that the DCS DC drive technology does not have adequate torque regulation to perform dancer position regulation. Further it will be shown that the performance of the position regulator is more of a system issue and strongly dependent on the performance of the speed loop rather than the performance of the current/torque loop.
A second issue that is resolved in this report is an explanation of observed dancer oscillations that occur at certain line-speeds and roll diameters. It will be shown that these oscillations occur when the frequency of the once-per-revolution disturbance introduced into the system by an egg-shaped roll on the test system backstand that feeds web to the dancer regulated turret winder, coincides with the web/system-inertia natural frequency, or a harmonic of the same. The backstand diameter/line speed combinations that cause this phenomena can be predicted, and correlated with field data.
NOMENCLATURE:
|
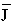 = =
|
Per normal inertia [sec]. (see RSP 30.002) |
|
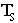 = =
|
The Scan Time (default = .005) [sec] |
|
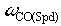 = =
|
The desired speed loop crossover frequency (default = 15 [rad/sec]) |
|
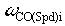 = =
|
The instantaneous speed loop crossover frequency |
|
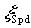 = =
|
The speed loop damping factor (default = 1.1) |
|
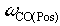 = =
|
The desired position loop crossover frequency (default = 5[rad/sec]) |
|
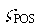 = =
|
The desired position loop damping factor (default =1) |
|
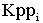 = =
|
The instantaneous position PI proportional gain = |
|
 = =
|
The instantaneous position PI lead frequency [rad/sec] |
|
 = =
|
The instantaneous position feedback lead frequency [rad/sec] |
|
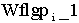 = =
|
The instantaneous position feedback lag frequency [rad/sec] |
|
Wcml = |
The Current/Torque Minor Loop (CML) bandwidth [rad/sec] |
|
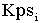 = =
|
The instantaneous SML PI proportional gain |
|
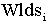 = =
|
the instantaneous SML PI lead frequency [rad/sec] |
|
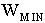 = =
|
Minimum strip width [in] |
|
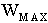 = =
|
Maximum strip width [in] |
|
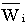 = =
|
Ratio of a given width to the maximum strip width |
|
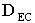 = =
|
Empty core diameter [ft] |
|
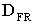 = =
|
Full roll diameter [ft] |
|
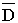 = =
|
The ratio of the full core diameter to the empty core diameter |
|
 = =
|
The ratio of a given core diameter to the empty core diameter |
|
 = =
|
Empty core inertia [lb ft^2] |
|
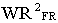 = =
|
Full roll inertia [lb ft^2] |
|
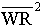 = =
|
The ratio of full roll inertia to the empty core inertia (with  ) ) |
|
 = =
|
The ratio of a given roll diameter inertia to the empty core inertia (with 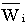 ) ) |
|
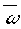 = =
|
Per-normal speed (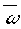 = 1 at base speed of motor) = 1 at base speed of motor) |
|
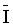 = =
|
Per-normal motor current (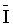 = 1 at rated current of motor) = 1 at rated current of motor) |
|
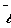 = =
|
Per-normal motor torque (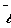 =1 at rated torque of motor) =1 at rated torque of motor) |
|
 = =
|
Motor Base speed [r.p.m.] |
|
 = =
|
Full-weakened field motor speed [r.p.m.] |
|
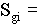
|
Application motor gear-in speed [r.p.m.] |
|
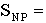
|
Nameplate motor base speed [r.p.m.] |
|
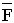 = =
|
The ratio of the fully weakened field motor speed to motor base speed |
|
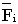 = =
|
The ratio of a given field weakened motor speed to the motor base speed. |
|
P_C = |
The Position loop percent control (expressed as a decimal i.e. 0 < P_C < 1) |
|
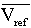 = =
|
per normal line speed reference (i.e. 1 = full line speed) |
|
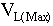 = =
|
Maximum line speed [in/sec] |
|
L = |
Storage [in] |
|
w f = |
Dominant second order web/system-inertia natural frequency [rad/sec] |
|
TH = |
Web thickness [in] |
|
Ri = |
Instantaneous roll radius [ft] |
|
d = |
Web material density [lb/ft^3] |
|
W = |
Web Width [in] |
|
E = |
Modulus of elasticity [psi] |
|
LEN |
Web length between backstand and winder [ft] |
Note: Storage is not always equal to the full amount of material that can be stored in the position controlled mechanical system. It is the amount of material that can be stored in the mechanical system over which the feedback varies from 0% to 100%.
 = The time it takes (in [sec]) to integrate storage to L [in] with = The time it takes (in [sec]) to integrate storage to L [in] with 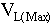 line speed. line speed.
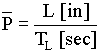 ; ;
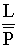 = The time it takes (in [sec]) to integrate storage to L [in] with = The time it takes (in [sec]) to integrate storage to L [in] with 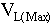 line speed. line speed.
For the sake of clarity the following diagram has been included to illustrate the relationship between  and L. and L.

Figure 1.  Description Description
Similarly for  : :
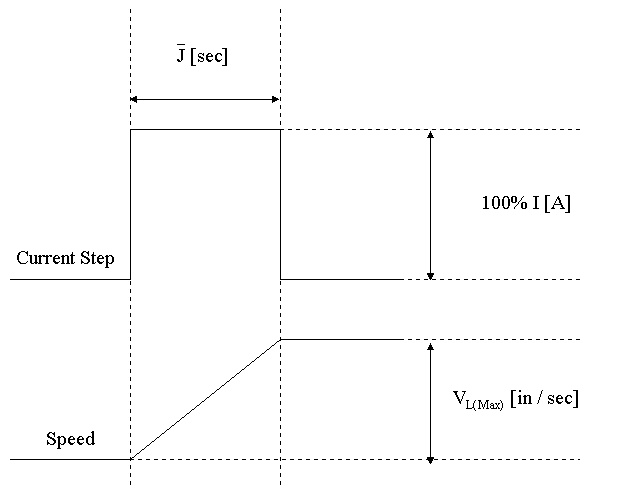
Figure 2.  Description Description
WINDER SPEED LOOP TUNING
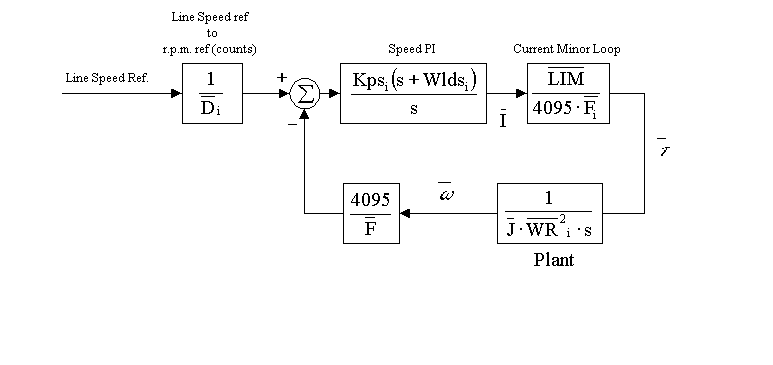
Figure 3. Winder Speed Loop Block Diagram
Fundamental Physical Equations:
Per-normal width:
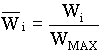 ; ;
Per-normal Diameter:
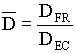 ; ; 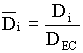 ; ; 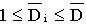
Per-normal Inertia:
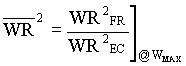 ; ; 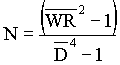 ; ; 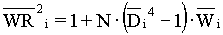 ; ; 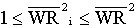
Per-normal field strength:
 ; ;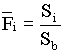 ; ;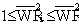
1-A) Speed Loop Open Loop Transfer Function
From Figure 3. the open loop transfer function is seen to be:
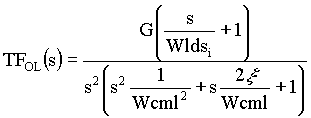 ,EQ. 1 ,EQ. 1
Where: G = 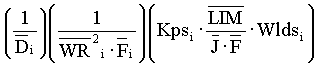 ,EQ. 2 ,EQ. 2
1-B) Closed Loop Transfer Function
Know: 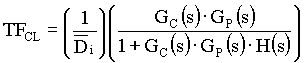 ,EQ. 3 ,EQ. 3
The following closed loop transfer function can be derived:
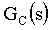 = =  ,EQ. 4 ,EQ. 4
 = =  ,EQ. 5 ,EQ. 5
 = = 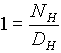 ,EQ. 6 ,EQ. 6
Therefore:
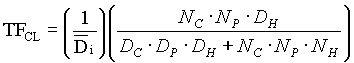 ,EQ. 7 ,EQ. 7
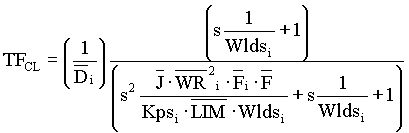 ,EQ. 7a ,EQ. 7a
Let: 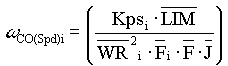 (this can be verified with analysis of the assymptotic bode plot. The derivation has been left out for the sake of brevity) using this substitution EQ. 7a becomes: (this can be verified with analysis of the assymptotic bode plot. The derivation has been left out for the sake of brevity) using this substitution EQ. 7a becomes:
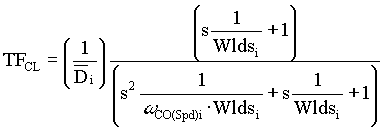 ,EQ. 7b ,EQ. 7b
EQ. 7b has the following denominator roots and damping factor:
 ,EQ. 8 ,EQ. 8
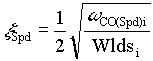 ,EQ. 9 ,EQ. 9
The roots of EQ. 8 become complex (i.e.  = 1) when = 1) when 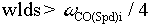 ; the best tuning for a winder speed loop uses a ratio of ; the best tuning for a winder speed loop uses a ratio of 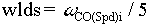 ; this yields an overshoot of approximately 10 %, It is interesting to note that the closed loop system is not critically damped as would be expected with a ; this yields an overshoot of approximately 10 %, It is interesting to note that the closed loop system is not critically damped as would be expected with a  > 1. This is due to the effect of adding a zero to the numerator of the 2nd order system (see a standard control text for more details). for a ratio of > 1. This is due to the effect of adding a zero to the numerator of the 2nd order system (see a standard control text for more details). for a ratio of 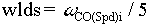 , ,  is set to 1.1 which is the default value for winder speed loops. is set to 1.1 which is the default value for winder speed loops.
From the above it can be easily seen that if the inertia of the system at empty core can be calculated, and the inertia at any given diameter can be calculated using the fundamental physical equations described above. We can tune the speed loop for any desired crossover and closed loop damping using this information. Further the calculated speed loop bandwidth can be used to adapt the tuning of the position loop so that it is optimally tuned for any given speed loop tuning. The above forms the fundamental reasoning behind the system identification test and speed loop auto-tuning that are described below:
Regulator Tuning
In most industrial winder applications the winder speed loop is tuned to maintain a crossover of 15 [rad/sec] as long as the forward gain term is less than 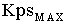 . The forward gain term must be limited in a given system so that drive shaft torque jitter does not dmage the mechanics of the winder, and does not excite drive shaft torsional dynamics. A good example of what torque jitter can do is illustrated in the following scenario. . The forward gain term must be limited in a given system so that drive shaft torque jitter does not dmage the mechanics of the winder, and does not excite drive shaft torsional dynamics. A good example of what torque jitter can do is illustrated in the following scenario.
Suppose that there is 0.2 % (or 10 [counts] out of the maximum 4095 [counts]) noise on the speed feedback. This noise is due to such phenomena as vibration in the machinery, (typically due to vibration in the drive train and feedback coupling etc.) and system noise from the process that is outside the bandwidth of the speed regulator. With a forward gain term of 60 and a current loop gain of 1.5 (or 150% rated motor current = max. possible current) the torque jitter on the motor shaft will equal 10 x 60 x 1.5 = 900 [counts] out of a maximum 4095 [counts] of current reference (i.e. about 40% of the rated torque). This torque jitter will stress the motor shaft and, if the torsional frquency is low enough and under-damped enough, excite and amplify the torsional resonance of the drive-shaft, usually damaging it.
The higher the bandwidth (Wcml) of the torque or current minor loop (CML) the more problematic this may become. This is especially true if AC vector or brushless DC drives with extremely high torque loop bandwidths are used in systems with large per-normal inertias.
Typically, in the ApICS LLC per-normal regulation scheme 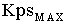 is chosen to be less than 60. Once is chosen to be less than 60. Once 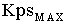 is reached is reached 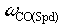 is reduced to maintain is reduced to maintain 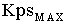 constant. Wlds is than adjusted accordingly to maintain the desired closed loop damping factor. The Figure 4. demonstrates how this is done. constant. Wlds is than adjusted accordingly to maintain the desired closed loop damping factor. The Figure 4. demonstrates how this is done.
Tuning Procedure:
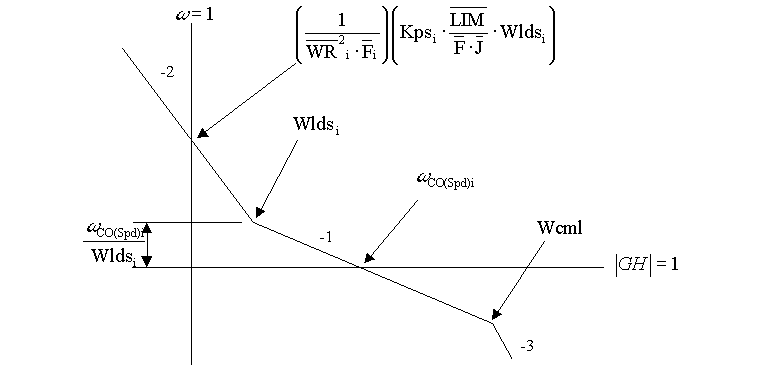
Figure 4. Winder Speed Loop Assymptotic Bode Plot
A basic statement is used to set Kpsi according to the following equation:
 ; ( ; (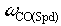 defaults to 15 [rad/sec]) defaults to 15 [rad/sec])
The following rules decide when to clamp Kps and lower the speed loop crossover as described above:
if: 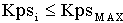 ; ( ; (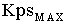 defaults to 60) defaults to 60)
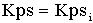
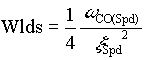 ( (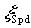 defaults to 1.1) defaults to 1.1)
else: 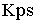 = = 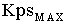

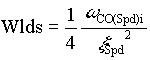 ( (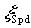 defaults to 1.1) defaults to 1.1)
"J_Bar" ID test and the auto-tuning feature
From Figure 2. it is clear that if we put a 100% current step into the CML and measure the time it takes to reach base speed, 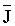 can be calculated. While the test we perform at empty core and with a large roll is not quite that simple, that is the main idea behind it. The goal of these two test is to take information from several current loop step and speed feedback data sets and calculate the coefficients required to estimate per-normal inertia at any point in the coil build-up as a function of diameter. The nice feature of doing this with an on-site identification algorithm is that air-entrainment is taken into account in the final coefficient set and the calculated inertia calculation more closely matches the actual than does the theoretical, which does not take air-entrainment into account. We have found the results to be very robust. This test is performed on-site in approximately 2 - 3 hours, after which the plant is identified and the speed loop can be auto-tuned using the equations in the tuning section above. can be calculated. While the test we perform at empty core and with a large roll is not quite that simple, that is the main idea behind it. The goal of these two test is to take information from several current loop step and speed feedback data sets and calculate the coefficients required to estimate per-normal inertia at any point in the coil build-up as a function of diameter. The nice feature of doing this with an on-site identification algorithm is that air-entrainment is taken into account in the final coefficient set and the calculated inertia calculation more closely matches the actual than does the theoretical, which does not take air-entrainment into account. We have found the results to be very robust. This test is performed on-site in approximately 2 - 3 hours, after which the plant is identified and the speed loop can be auto-tuned using the equations in the tuning section above.
WINDER POSITION LOOP TUNING
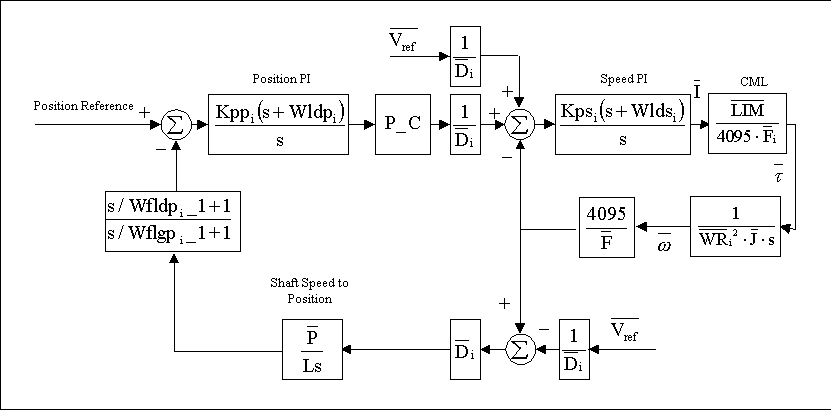
Figure. 5 Linearized Block Diagram of a Winder Position Loop Control Scheme
Open Loop Transfer Function
If we assume:
- The natural frequency of the dancer mass and web spring is significantly higher than the position loop crossover
- The closed speed loop damping is approximately 1
- There is no significant stiction in the dancer mechanism
- There is no significant backlash in the winder gearing
- There is no significant torsional wind-up in the gear train.
The position loop can be modeled with the following linear transfer function obtained from Figure 2.
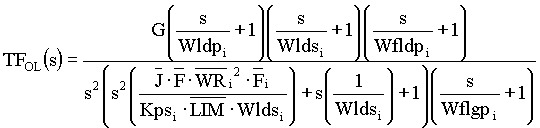 ,EQ. 10 ,EQ. 10
Where: G = 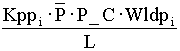 ,EQ. 11 ,EQ. 11
The closed speed loop can be approximated as a first order lag, with the lag set at the speed loop crossover frequency, that is:
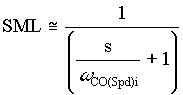 ,EQ. 12 ,EQ. 12
Resulting in the following open loop transfer function:
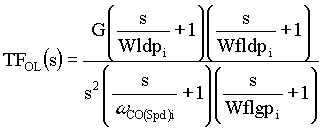 ,EQ. 13 ,EQ. 13
where: G = 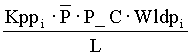 ,EQ. 14 ,EQ. 14
Tuning Procedure:
The winder position loop can be tuned for a desired crossover 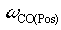 and a desired closed loop damping factor and a desired closed loop damping factor 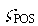 . The frequency and gain components of the position regulator are auto-tuned using these variables along with the speed loop crossover as calculated in the SML. Following are the equations used to tune the position loop. The derivation of these equations has been omitted for the sake of brevity. They are obtained by analysis of the open position loop bode plot. . The frequency and gain components of the position regulator are auto-tuned using these variables along with the speed loop crossover as calculated in the SML. Following are the equations used to tune the position loop. The derivation of these equations has been omitted for the sake of brevity. They are obtained by analysis of the open position loop bode plot.
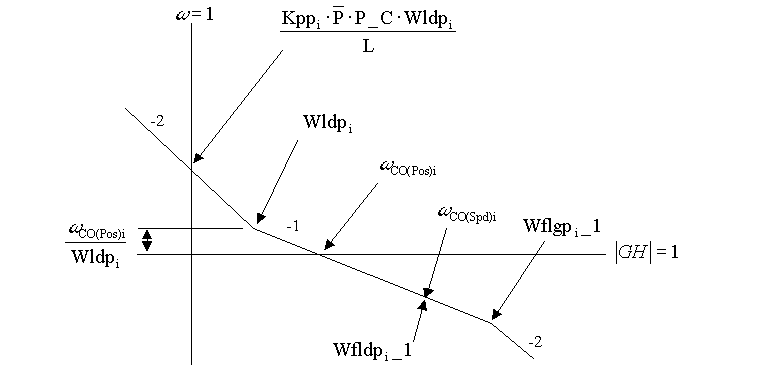
Figure 6. Design B Asymptotic Open Loop Bode Gain Plot
i) The PI lead frequency, Wldp is set to yield adequate phase margin @ 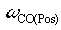 , it moves with the position loop damping ( , it moves with the position loop damping (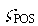 ) to adjust phase margin at the position loop crossover such that the desired position loop damping is obtained setting as follows: ) to adjust phase margin at the position loop crossover such that the desired position loop damping is obtained setting as follows:
Wldp = 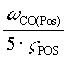 [rad/sec] ( [rad/sec] (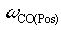 defaults to 5 [rad/sec]),EQ. 15 defaults to 5 [rad/sec]),EQ. 15
ii) The PI regulator proportional gain term is obtained as:
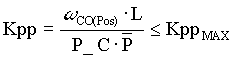 ( ( defaults to 5),EQ. 16 defaults to 5),EQ. 16
iii) The feedback lead/lag lead, Wfldp_1_i is set to approximately cancel the closed speed loop lag @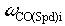 , it also moves with the position loop damping ( , it also moves with the position loop damping (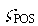 ) setting to adjust phase margin at the position loop crossover such that the desired position loop damping is obtained. That is: ) setting to adjust phase margin at the position loop crossover such that the desired position loop damping is obtained. That is:
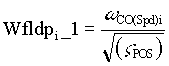 ,EQ. 17 ,EQ. 17
iv) The feedback lead/lag lag, Wflgp_1_i is be set at 20 times the lead/lag feedback frequency with the following limitation. The lag frequency must be less than 1.2/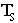 [rad/sec], this is due to sampling/aliasing limitations: [rad/sec], this is due to sampling/aliasing limitations:
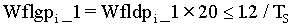 [rad/sec],EQ. 18 [rad/sec],EQ. 18
A SHORT DISCUSSION REGARDING POSITION LOOP PERFORMANCE AND RELATED DEPENDENT FACTORS
For winder position regulators where the bandwidth of the SML is very low due to large per-normal inertias reflected to the motor shaft at or near a full roll operating condition, the position loop stability and bandwidth is strictly dependent on the correct setting of the lead/lag compensation in the position feedback as a function of the speed loop bandwidth. The factor limiting speed loop bandwidth under these operating conditions is not dependent on the bandwidth of the current/torque minor loop, rather it is limited by torque jitter requirements as described previously. For example:
Given that the per-normal inertia of a system at empty core is 1 [sec] (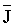 = 1) and at full-roll is 20 [sec] ( = 1) and at full-roll is 20 [sec] ( =20) and you want to limit your forward path gain to 60 with a closed loop current loop gain of 1.5 ( =20) and you want to limit your forward path gain to 60 with a closed loop current loop gain of 1.5 ( =1.5), assume a field range of 4:1 over build-up. In addition your field will be at max. strength ( =1.5), assume a field range of 4:1 over build-up. In addition your field will be at max. strength (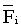 =1) at full roll, therefore your bandwidth is physically limited to : =1) at full roll, therefore your bandwidth is physically limited to :
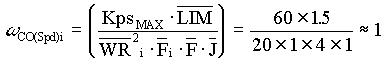 [rad/sec], EQ. 19 [rad/sec], EQ. 19
If you have a current/torque minor loop with a bandwidth of 200 [rad/sec] (such as the DCS DC drive) or 1000 [rad/sec] (such as you would have with a DCS brushless or vector drive) it will make absolutely no difference to the performance of the speed loop, both are orders of magnitude higher than the bandwidth of the speed loop. Similarly the performance of the position loop will not be enhanced by choice of either drive technology, rather, the position loop must have a suitable adaptation algorithm to ensure stable operation over the expected range of inertias and speed loop crossovers. We at ApICS LLC are, to my knowledge, the only industrial control system analytical consultants that currently offer these adaptive algorithms.
One way to avoid having to use this adaptation algorithm is to use a larger HP motor. But in the paper and film industry low tension requirements do not require large HP motors on their winders for steady state running conditions. Therefore the need exists in these applications for the described position regulation scheme.
O.E.M./MANUFACTURER WINDER APPLICATION ANALYSIS
The following linear analysis was performed using MATLAB and proprietary control system analysis software.
The analysis consists of two sections. The first section is an analysis of the "current technology" fixed speed and position loop gain regulation scheme, the second section is an analysis of the proposed adaptive speed and position loop regulation scheme. Each section contains the following set of plots:
- Plot of per-normal field strength, per-normal inertia, speed loop crossover, speed loop lead frequency and speed loop proportional gain versus per-normal diameter. This plot shows how speed loop bandwidth varies with buildup and field strength.
- Plot of per-normal field strength, per-normal inertia, and per-normal current versus per-normal diameter for a fixed web tension and acceleration rate. This plot shows the expected per-normal current required to accelerate the winder to top line speed at any given diameter while maintaining the specified web tension.
- Open-loop Bode plot of the position loop at empty core
- Closed-loop Bode plot of the position loop at empty core
- Position reference unit step response plot at empty core
- Disturbance unit step response plot at empty core(this is equivalent to observing the position loop response to a unit step response in the speed of the line master bridle)
- Open-loop Bode plot of the position loop at full roll
- Closed-loop Bode plot of the position loop at full roll
- Position reference unit step response plot at full roll
- Disturbance unit step response plot at full roll
Note: The step responses have two traces on each plot the most "peaky" trace is a plot of the position loop feedback after the lead/lag block (or at the summing junction of the position regulator) The less "peaky" trace is a plot of the actual control variable (or the actual dancer position).
FIXED SPEED & POS. LOOP GAIN SYSTEM STABILITY ANALYSIS
Motor Parameters:
|
Nameplate Base Speed |
1730 [r.p.m] |
|
Motor Maximum Speed |
3000 [r.p.m] |
|
Motor Power |
15 [HP] |
|
Torque at LIM Current |
69.3 [ft*lbf ] |
|
Motor WR^2 |
10.03 [lb ft^2] |
|
Motor Design Number |
DG6702B |
Motor Field Curve Parameters:
|
Point |
Speed [r.p.m.] |
Field Current [A] |
|
1 |
1730 |
1.28 |
|
2 |
1889 |
1.16 |
|
3 |
1968 |
1.11 |
|
4 |
2048 |
1.07 |
|
5 |
2127 |
1.03 |
|
6 |
2206 |
0.99 |
|
7 |
2286 |
0.95 |
|
8 |
2365 |
0.92 |
|
9 |
2444 |
0.89 |
|
10 |
2524 |
0.86 |
|
11 |
2603 |
0.84 |
|
12 |
2683 |
0.81 |
|
13 |
2762 |
0.79 |
|
14 |
2841 |
0.76 |
|
15 |
2921 |
0.74 |
|
16 |
3000 |
0.72 |
Winder Physical Parameters
|
Minimum Web Width |
50 [in] |
|
Maximum Web Width |
76 [in] |
|
Minimum Roll Diameter (EC) |
6.5 [in] |
|
Maximum Roll Diameter (FR) |
36 [in] |
|
Storage |
6 [in] |
|
Gear Ratio |
5 |
|
Line Accel. Time |
20 [sec] |
|
Maximum Line Speed |
1000 [ft/min] |
|
Product Density |
0.039 [lb/in^3] |
|
Mandrill Inside Diameter |
0 [in] |
|
Mandrill Outside Diameter |
6 [in] |
|
Mandrill Length |
80 [in] |
|
Mandrill Density (Aluminium) |
0.0873 [lb/in^3] |
|
Product Reflected WK^2 |
135.6 [lb*ft^2] |
|
Mandrill Reflected WK^2 |
0.2 [lb*ft^2] |
|
Gear WK^2 |
1.0 [lb*ft^2] |
|
Motor WK^2 |
> 10.0 [lb*ft^2] |
|
Reflected Fixed WK^2 |
> 12.3 [lb*ft^2] |
|
Reflected Total (FR) WK^2 |
> 147.9 [lb*ft^2] |
17 pt. Calculated Product Reflected WK^2 (Inertia) Table Values:
|
Point |
WK^2 [lbf*ft^2] |
WK^2 [PN] |
D_Bar |
|
0 |
0.00 |
0 |
1.00 |
|
1 |
0.25 |
83 |
1.28 |
|
2 |
0.73 |
245 |
1.57 |
|
3 |
1.55 |
522 |
1.85 |
|
4 |
2.85 |
961 |
2.13 |
|
5 |
4.79 |
1614 |
2.42 |
|
6 |
7.55 |
2542 |
2.70 |
|
7 |
11.32 |
3813 |
2.99 |
|
8 |
16.34 |
5504 |
3.27 |
|
9 |
22.85 |
7696 |
3.55 |
|
10 |
31.12 |
10482 |
3.84 |
|
11 |
41.44 |
13959 |
4.12 |
|
12 |
54.13 |
18233 |
4.40 |
|
13 |
69.52 |
23418 |
4.69 |
|
14 |
87.97 |
29635 |
4.97 |
|
15 |
109.87 |
37012 |
5.25 |
|
16 |
135.62 |
45685 |
5.54 |
Assuming Losses of 10 percent Max. Possible Web Tension [lb] at Important Roll Diameters
|
Condition |
Regen. |
Mot |
@Dia. |
Line Spd. |
|
Full Roll |
167 |
137 |
36.0 [in] |
1000 [ft/m] |
|
Torque Taper |
544 |
445 |
11.0 [in] |
1000 [ft/m] |
|
Empty Core |
544 |
445 |
6.5 [in] |
1000 [ft/m] |
This
Notes:
- Adequate tension capability exists for the entire range of expected tension taper profiles.
- Torque taper point is the point in the build-up where the motor field strength reaches maximum. From this point on the max. possible tension drops of with larger diameters.
Regulator Parameters:
|
Lim Bar (LIM) |
1.5 |
|
Scan Time |
0.01 [sec] |
|
CML Crossover |
200 [rad/sec] |
|
Kps |
50.0 |
|
Wlds |
0.3 [rad/sec] |
|
Kpp |
2.0 |
|
Wldp |
2.0 [rad/sec] |
|
Wfldp_1 |
12 @ Empty Core,
1.5 @ Full Roll |
|
Wflgp_1 |
Twice Wfldp_1 |
|
Position Loop % Control |
10 % |
|
F_Bar |
1.70 |
|
WR2_Bar |
12.04 |
|
D_Bar |
5.54 |
|
W_Bar |
0.66 |
|
J_Bar |
1.52 [sec] |
|
J_Bar of the Motor |
1.24 [sec] |
|
Storage/P_Bar |
0.03 [sec] |
|
Empty Core SML Crossover |
15.0 [rad/sec] |
|
Full Roll SML Crossover |
2.9 [rad/sec] |
|
Calculated Base Speed |
1730 R.P.M. |
|
Calculated Gear-in Speed |
2938 R.P.M. |
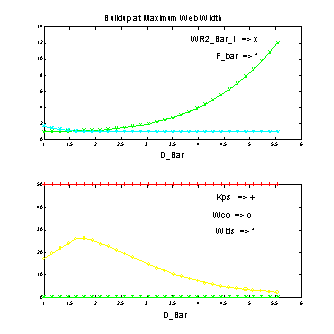
Figure 7. Current Technology SML Crossover Versus PN Diameter.
In Figure 7. the bandwidth of the speed loop can be seen to vary from a high of approximately 27 [rad/sec] to a low of 2.9 [rad/sec]. It is quite possible that the machine may be damaged over time with the speed loop bandwidth that is observed at D_Bar = 1.75. Torsional problems may also be excited. In addition the damping of the speed loop (proportional to the ratio of 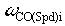 /Wlds_i) is changing over build-up. /Wlds_i) is changing over build-up.
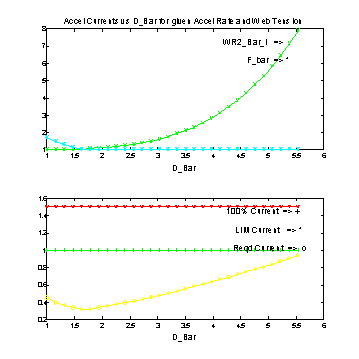
Figure 8. Current Technology Acceleration Currents Versus PN Diameter
Figure 8. shows the current required to accelerate the winder to top speed (1000 [ft/min]) in 20 [sec] with 115 [lbf] of load tension applied to the web over the build-up range. It also shows that there is plenty of HP in the motor to meet the specified acceleration time and tension specification.
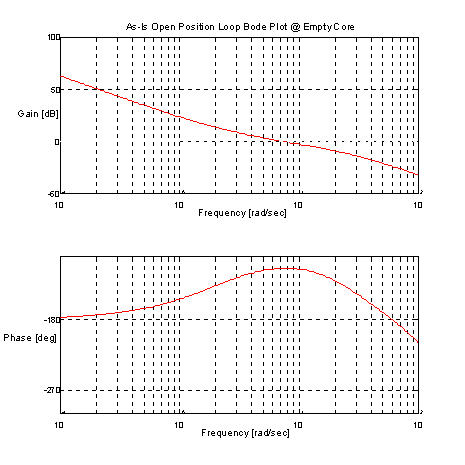
Figure 9. Current Technology Open Loop Bode Plot @ Empty Core
The Position Loop open loop bode plot in Figure 9. indicates that the position loop crossover occurs @ approx. 7 [rad/sec] with a phase margin of 63 [deg]. This is a stable operating condition.
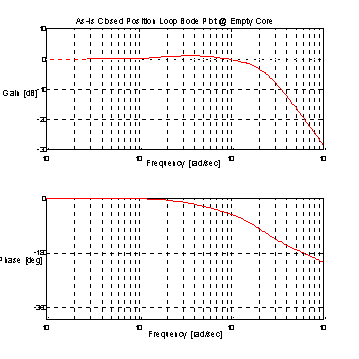
Figure 10. Current Technology Closed Loop Bode Plot @ Empty Core
In Figure 10. we see the "flattened" closed loop bode plot characteristic of a well designed regulator. From this we can conclude that the Current Technology design is quite adequate at empty core.
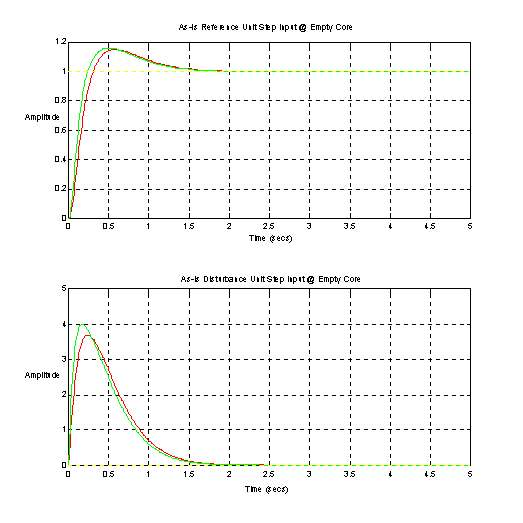
Figure 11. Current Technology Empty Core Step Responses
As predicted by the closed loop bode plot (Figure 10) the step responses are well behaved at empty core.
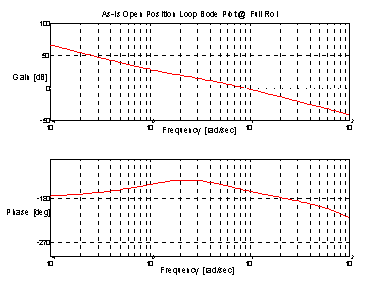
Figure 12. Current Technology Open Loop Bode Plot @ Full Roll
The Position Loop open loop bode plot in Figure 12. indicates that the position loop crossover occurs @ approx. 9 [rad/sec] with a phase margin of 17 [deg]. This is a marginally stable operating condition. It is very easy to believe that a small variation in the plant would result in system instability. Typically control systems are designed with AT LEAST 45 [deg] phase margin.
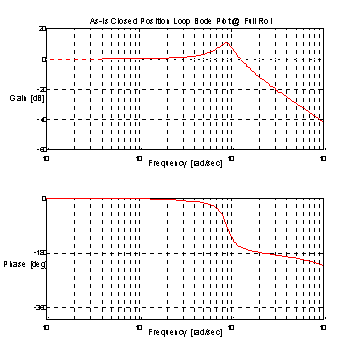
Figure 13. Current Technology Closed Loop Bode Plot @ Full Roll
The peaky closed loop response shown in Figure 13. indicates that this Current Technology operating condition (full roll) is marginally stable.
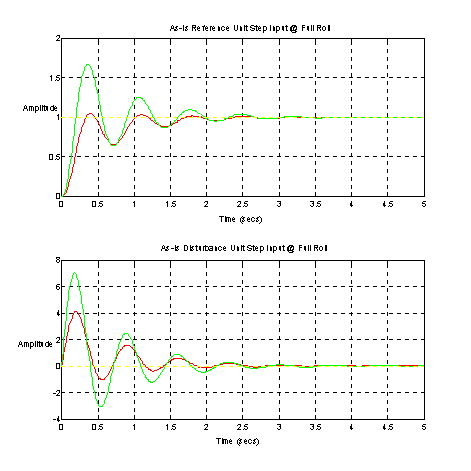
Figure 14. Current Technology Full Roll Step Responses
As predicted by the closed loop bode plot (Figure 13) the full roll step responses are oscillatory and very under-damped.
PROPOSED ADAPTIVE SPEED & POS. LOOP SYSTEM STABILITY ANALYSIS
All mechanical parameters are the same as for the Current Technology analysis.
Regulator Parameters:
|
Lim Bar (LIM) |
1.5 |
|
Scan Time |
0.01 [sec] |
|
CML Crossover |
200 [rad/sec] |
|
Kps_Max |
50.0 |
|
Kpp_Max |
5 |
|
Kps |
Adaptively Tuned |
|
Wlds |
Adaptively Tuned |
|
Kpp |
Adaptively Tuned |
|
Wldp |
Adaptively Tuned |
|
Wfldp_1 |
Adaptively Tuned |
|
Wflgp_1 |
Adaptively Tuned |
|
Position Loop % Control |
10 % |
|
F_Bar |
1.70 |
|
WR2_Bar |
12.04 |
|
D_Bar |
5.54 |
|
W_Bar |
0.66 |
|
J_Bar |
1.52 [sec] |
|
J_Bar of the Motor |
> 1.24 [sec] |
|
Storage/P_Bar |
> 0.03 [sec] |
|
Empty Core SML Crossover |
> 15.0 [rad/sec] |
|
Full Roll SML Crossover |
> 2.9 [rad/sec] |
|
Calculated Base Speed |
> 1730 R.P.M. |
|
Calculated Gear-in Speed |
> 2938 R.P.M. |

Figure 15. Proposed SML Crossover Versus PN Diameter
Figure 15. clearly demonstrates the adaptive nature of the proposed SML. Kps can be seen to vary while the speed loop crossover (Wco) remains constant up until D_Bar = 3. At the point where the speed loop Kps_Max point (50) is reached, the speed loop bandwidth drops of but at the same time the lead frequency (Wlds) lowers to maintain a constant damping of approximately 1 in the SML.

Figure 16. Current Technology Acceleration Currents Versus PN Diameter
Figure 16., like figure 8, shows that there is plenty of HP in the motor to meet the specified acceleration time and tension specification (115 [lb] tension, 20 [sec] to 1000 [ft/min])
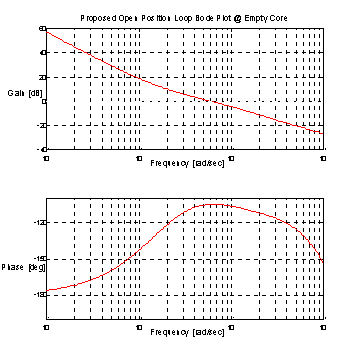
Figure 17. Proposed Open Loop Bode Plot @ Empty Core
The Position Loop open loop bode plot in Figure 17. indicates that the position loop crossover occurs @ approx. 6 [rad/sec] with a phase margin of 75 [deg]. This is a very stable operating condition.

Figure 18. Proposed Closed Loop Bode Plot @ Empty Core
In Figure 18. we see the "flattened" closed loop bode plot characteristic of a well designed regulator. From this we can conclude that the proposed design is more than adequate at empty core.
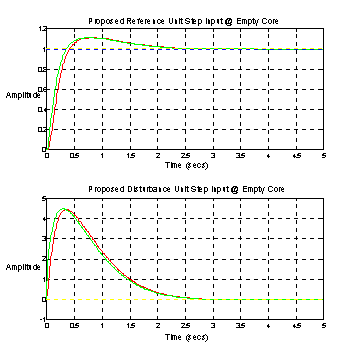
Figure 20. Proposed Empty Core Step Responses
As predicted by the closed loop bode plot (Figure 19) the step responses are well behaved at empty core.
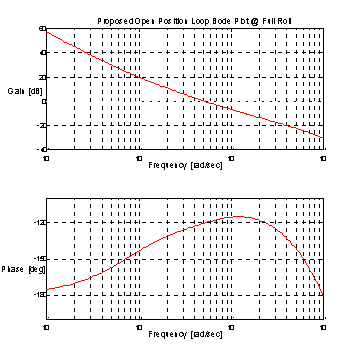
Figure 21. Proposed Open Loop Bode Plot @ Full Roll
The Position Loop open loop bode plot in Figure 21. indicates that the position loop crossover occurs @ approx. 5 [rad/sec] with a phase margin of 60 [deg]. This is a still a very stable operating condition unlike that shown in Figure 9.
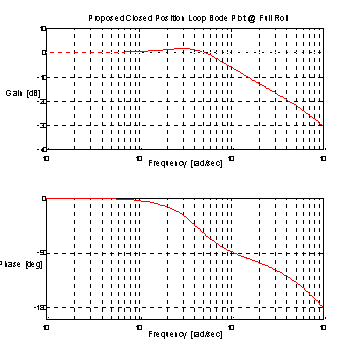
Figure 22. Proposed Closed Loop Bode Plot @ Full Roll
In Figure 22. we see the "flattened" closed loop bode plot characteristic of a well designed regulator. From this we can conclude that the proposed design is more than adequate at full roll unlike the Current Technology design as shown in Figure 10.
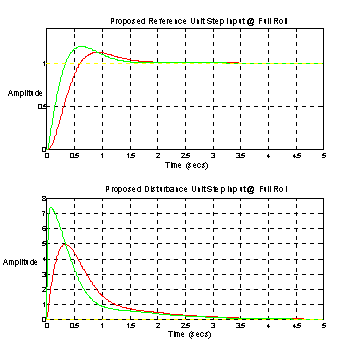
Figure 23. Proposed Full Roll Step Responses
As predicted by the closed loop bode plot (Figure 22) the step responses are well behaved at full roll.
EXPLANATION OF OBSERVED DANCER OSCILLATIONS AT SPECIFIC SPEEDS AND ROLL DIAMETERS
The OEM/Manufacturer Engineers expressed concerns about observed dancer oscillations at specific line speeds and roll diameters. The following explanation describes why these oscillations occur, and what can be done to correct them.
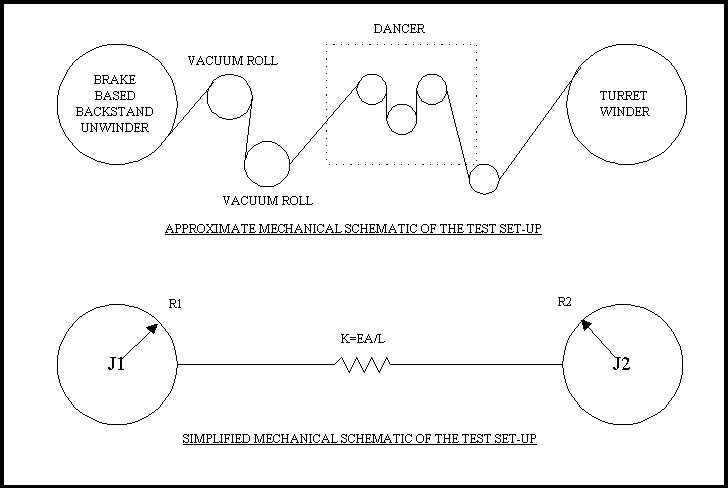
Figure 24. Approximate Mechanical Schematic
Figure 24 shows approximate mechanical schematics of the test system where the described problem was observed. The simplified schematic showing two inertias and one web "spring" is a classic two mass spring system with a natural frequency wf of:
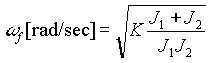 where: where: 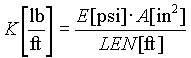 ; EQ. 20 ; EQ. 20
The inertia of each roll will vary with diameter as follows:
 ; EQ. 21 ; EQ. 21
The instantaneous winder/un-winder inertias are calculated using the instantaneous roll diameters:
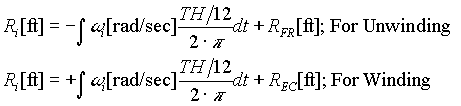 ; EQ. 22 ; EQ. 22
Where RFR is the initial condition full roll radius of the backstand roll, and REC is the initial condition empty core roll radius of the winder, and wi is the instantaneous roll rotational speed in units of [rad/sec].
The winder or unwinder roll surface speeds are calculated as a function of the motor rotational speed, the gear ratio, and the instantaneous roll radius:
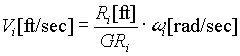 ; EQ. 23 ; EQ. 23
Equations 20 - 23 describe how the time-varying dominant second-order natural frequency of the approximate 2 mass - 1 spring system varies. The instantaneous value of the natural frequency will depend on the instantaneous value of each roll. As the backstand unwinds, and feeds the turret winder, its inertia J1 will decrease as the roll radius R1 decreases. The equation describing the decrease in the backstand roll radius is given by EQ. 22 (Unwinding). At the same time, the winder inertia J2 and winder roll radius R2 will increase, as described by EQ. 21 and EQ. 22 (Winding). Substituting the instantaneous calculated values of J1 and J2 (from EQ 21 using the radii calculated in EQ. 22) into EQ. 20 will yield an approximation of the instantaneous dominant natural frequency of the line for that instant in time.
Assuming that there exist imperfections in the roll on the backstand (usually an "egg-shaped" roll) a once-per-revolution (or occasionally a twice-per-revolution) disturbance will be introduced into the process. This disturbance can be heard as a noticeable audible "thump". The disturbance results from a rapid change in the exit speed of the web as it leaves the roll. The magnitude of these variations in roll surface exit speed (DVi) are proportional to the given line speed and the magnitude of the variation in roll diameter as shown in EQ. 24
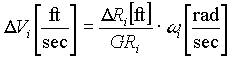 ; EQ. 24 ; EQ. 24
Where wi = the calculated motor speed for a given line speed and roll diameter.
The frequency wD of this disturbance will depend on the line speed and the roll diameter:
 ; EQ. 25 ; EQ. 25
If the unwind roll is NOT fed into a dancer then a tension disturbance will result. For example, a system in which a tension regulated unwind feeds into a speed regulated bridle or calendar. The magnitude of the tension disturbance is then directly proportional to the elasticity of the material, and the change in roll surface described in EQ. 26. Frequency components of the disturbance that are outside the bandwidth of the tension regulator will pass directly into the process through the speed regulated bridle.
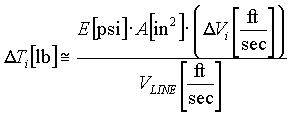 ; EQ. 26 ; EQ. 26
In this test application the torque regulated (brake torque) backstand was fed directly into a pair of speed regulated vacuum rolls, and then into the dancer that is regulated by the turret winder dancer loop. The small variations in surface speed, and the resulting tension deviations, will act on the dancer THROUGH the length of web attaching the dancer to the backstand. This is an important point to consider when we look at the effect of this disturbance on the system as a function of the natural frequency of the two inertia single spring system approximation described earlier.
Frequency components of the disturbance that are outside the bandwidth of the position regulator will not be compensated for by the position regulator, and, when this is the case, the dancer will be observed to oscillate at the same frequency as the disturbance (i.e. "in-sync" with the once-per-revolution disturbance of the backstand).
When the frequency of the disturbance wD (EQ. 25) coincides with the dominant second order natural frequency of the system wf (EQ. 20), the injection of energy into the closed system at the same frequency as the system natural frequency will stimulate the two inertias (i.e the backstand and the winder rolls) to exchange energy through the web that couples them together. Again, if the frequency components of the disturbance are outside the bandwidth of the position regulator they will not be compensated for by the position regulator, and consequently, the magnitude of the dancer oscillations will increase. The magnitude of the increase in the oscillations will depend on the elasticity of the material in the system. The more elastic, the greater the "stretch" of the material that will take place, and consequently the greater the movement of the dancer. The magnitude of the expected variation in dancer position is not easily quantified due to the non-linear stress-strain relationship associated with film and other plastic based materials.
To alleviate the problems associated with this phenomena when testing the turret winder, the operator can either slow down or speed up the machine when the oscillations occur, to ensure that the instantaneous disturbance frequency wD (or its second harmonic) does not coincide with the instantaneous system natural frequency at that instant in time. After 20 - 40 seconds, the desired line speed may be resumed.
Alternatively, the brake based backstand can be replaced with a drive based system, and a very light (i.e. low loading) dancer installed on the backstand. This will help to isolate the disturbance from the winder system.
CONCLUSIONS
The above analysis demonstrates the effectiveness of the proposed dancer position regulation scheme and demonstrates the advantages inherent in applying adaptive speed and position loop algorithms in winder dancer applications. Current dancer regulation schemes have proven inadequate. In these applications, the need for bandwidth in the dancer position loop (due to limited dancer storage) cannot be satisfied. This is due to instability in the position loop that results from the degraded fixed gain SML bandwidth as the roll builds up. The proposed scheme has proven to be of great benefit when these two seemingly contradictory requirements arise.
As a closing note, the stability of the position loop in winder applications is not dependent on the drive technology that is used. This is especially true for winders in the paper and film industries where per-normal inertias can, and are, very large at full roll and small at empty core. In fixed inertia servo position loops the per-normal inertia is small and the resulting speed loop bandwidths are high. In these applications torque loop response can be critical.
The oscillations observed in the dancer at certain line speeds and backstand roll diameters occurs when the frequency of the once-per-revolution backstand out-of-shape roll is coincident with the 2nd order dominant natural frequency of the system. To alleviate the problems associated with this phenomena the operator can either slow down or speed up the machine when the oscillations occur, to ensure that the frequencies are not co-incident.
|