APPLIED INDUSTRIAL CONTROL SOLUTIONS
ApICS LLC.
Winder Tension Control Simulation
&
A Robust Winder Tension Control Algorithm
B. T. BOULTER
© ApICS ® LLC 2000
ABSTRACT
This engineering study, satisfies the requirements prescribed in Systems Engineering Proposal "CLUTCH TENSION CONTROL SIMULATION AND DEVELOPMENT OF A ROBUST TENSION CONTROL ALGORITHM" Brief sets of results that reflect the expected system performance are provided. Included is a brief description of the simulation sub-systems. The simulation description is meant to provide the user with the information required to perform "what-if" scenarios using the simulation.
A detailed description of the control algorithm and all difference equations used in the simulation are also described.
INTRODUCTION
Scope
The scope of this document is limited to a brief description of the first principal equations describing the system, providing an overview of the simulation and the control structure sub-systems, and providing a detailed description of the control algorithm, including all necessary difference equations.
Results
Brief sets of results that provide insight into the expected behavior of the system with varying system configurations are included.
For each presented result, the following variables are plotted:
- Web Tensions [lb]
- Backstand/Winder torque [lb ft]
- Line speed [ft/min]
- Roll Diameter [in], and Inertia [lb ft2]
The investigations include: the effect of roll diameter on gain adaptation response time, demonstration of stable response over the entire roll build-up/wind-down. Demonstration of stable operation over a wide range of material thicknesses and elasticities.
A procedure for starting up the regulator is described, along with necessary sequencing issues that must be implemented for the regulator to operate in a safe manner.
The study concludes with some pertinent observations, and conclusions/recommendations.
CHAPTER 1
PLANT FIRST PRINCIPAL EQUATIONS
OVERVIEW
Figure 1. describes the system under study. Equations (1.1) through (1.8) describe the system shown in figure 1, with the inclusion of non-linear relationships between state variables that are not obvious from the figure.
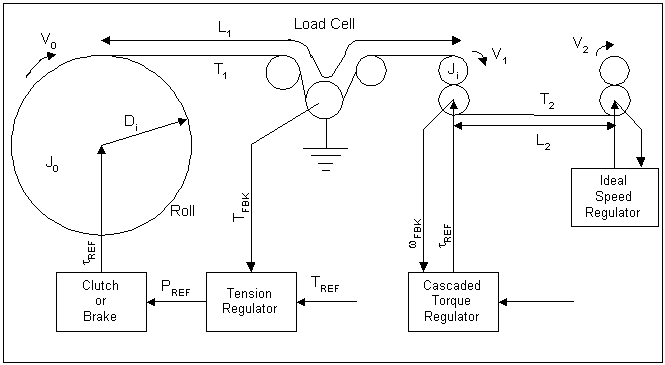
Figure 1. System Diagram
The ideal speed regulator provides the exit velocity for the second web span, a cascaded torque regulator (i.e. a torque regulator that is cascaded around a speed regulator) is included to dampen the dynamics between the stiff speed source and the winder/backstand dancer zone.
Nomenclature
|
S |
The Laplace operator |
|
J 0 |
The roll plus brake/clutch inertia [lb ft^2] |
|
J 1 |
The motor + roll inertia of the cascaded torque regulated roll [lb ft^2] |
|
VI |
The iíth roll surface velocity [ft/min] |
|
w I |
The i'th roll rotational velocity feedback [rad/sec] |
|
B V |
Viscous friction [lb ft sec / rad] |
|
B C |
Coulomb friction force [lb ft sec / rad] |
|
B S |
Stiction friction force [lb ft sec / rad] |
|
RI |
The iíth roll radius [ft] |
|
REC |
Empty core radius [ft] |
|
RFR |
Full roll radius [ft] |
|
DEC |
Empty core diameter [ft] |
|
DFR |
Full roll diameter [ft] |
|
WKEC |
Empty core inertia [lb ft^2] |
|
WKFR |
Full roll inertia [lb ft^2] |
|
GRI |
The iíth roll gear ratio |
|
LI |
The iíth tension zone length [ft] |
|
LFixed |
Length of material in winder/backstand span |
|
TI |
The iíth tension zone tension [lb] |
|
t I |
The iíth shaft torque [lb ft] |
|
EI |
Web modulus of elasticity [PSI] |
|
EMOD |
Base web Modulus of elasticity [PSI] |
|
AI |
Web cross sectional area [in^2] |
|
W |
Web width [ft] |
|
d |
Material density [lb/ft^3] |
|
TH |
Material thickness [in] |
|
TREF |
Tension reference [lb] |
|
TS |
Sample rate [sec] |
First Principal Equations
The following equations describe the physical system.
Web Tension Equations
(1.1-4) describe the relationship between entry and exit web velocities and tension in a web span for the two web spans in the simulation of a winder.
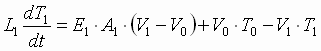 (1.1) (1.1)
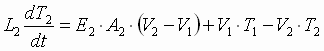 (1.2) (1.2)
For a backstand:
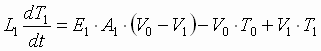 (1.1a) (1.1a)
 (1.2a) (1.2a)
Where:
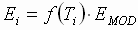 (1.3) (1.3)
The proprietary non-linear equation f(Ti) describing the variation of web modulus of elasticity as a function of the web tension, or web strain to be more precise, closely mimics the non-linear behaviour of plastic non-deformable web material. The assumption is made that the strain in the material is limited such that deformation does not take place.
The non-linear power terms 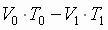 are often ignored when modeling web processes. Ignoring these terms enables the integration algorithm to converge more quickly and results in faster simulation times. Given that this study is not prescribed to undertake a detailed study of web dynamics, and in order to facilitate a more rapid simulation, these terms have been dropped from the system simulation. are often ignored when modeling web processes. Ignoring these terms enables the integration algorithm to converge more quickly and results in faster simulation times. Given that this study is not prescribed to undertake a detailed study of web dynamics, and in order to facilitate a more rapid simulation, these terms have been dropped from the system simulation.
Torque Equations:
The equations describing the relationship between torque, rotational speed, and roll surface speeds are typically non-linear in nature. To assist in the description of these non-linear equations a linearized model is first described, then the modifications to the linearized model are presented.
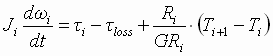 ; (1.5) ; (1.5)
The loss torque is a non-linear contribution that is a function of the magnitude and direction of the shaft speed. Equation (1.6) is a popular model that adequately represents the non-linear aspects of friction. It is from standard tribology texts on the subject [1],[2].
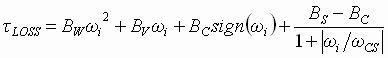 (1.6) (1.6)
Only viscous friction was included in this simulation.
The Winder/Backstand torque equations have time varying inertia, and surface speed characteristics. The following equations describe this phenomena.
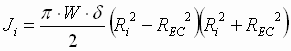 ; (1.7) ; (1.7)
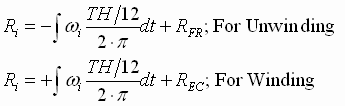 ; (1.8) ; (1.8)
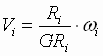 ; (1.9) ; (1.9)
Simulation Controller structure
There are two regulators in the simulation;
- The tension regulation regulator
- The cascaded torque regulator
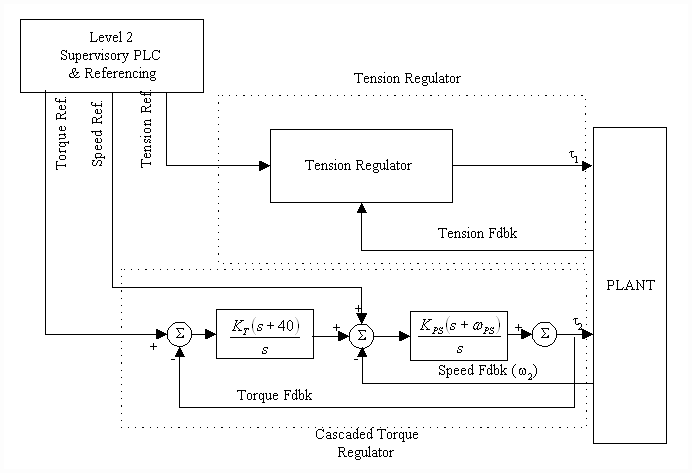
Figure 3. Controller Structure
Cascaded Torque Regulator
The cascaded torque regulator is tuned for a speed loop bandwidth of 5 [rad/sec] and a torque loop bandwidth of 5 [rad/sec].
Tension Regulator
The Tension Regulator description is protected by an IP agreemenet. It does contain an adaptive frequency based adaptation algorithm. The following discussion explains the need for this approach:
The Need for Frequency Adaptation
In Figures 7.b & 7.c below, plots graphing the change in the normalized (i.e. empty core natural frequency = 1 [rad/sec]) dominant system natural frequency as a function of the variation in normalized roll diameter (i.e. empty core diameter = 1) is presented. The "shape" of this variation in natural frequency as a function of diameter depends on the ratio of the full roll inertia to the empty core inertia. In Figure 7a, a family of curves is shown for a Diameter ratio of 15:1 . In Figure 7b, a family of curves is shown for a Diameter ratio of 8:1. For both the graphs, the smallest inertia ratio is 2 :1, the largest is 300 : 1. From these figures it can be seen that to properly set-up the regulator, the right "mapping" of the natural frequency as a function of the estimated per-normal diameter must be identified. This implies that the approximate ratio of full roll to empty core inertia must be entered, and based on this, the proper mapping identified. The following equations are used to identify the normalized natural frequency.
Per-normal Diameter:
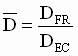 ; ;  ; ; 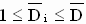 (1.13) (1.13)
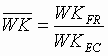 ; ; 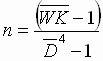 ; ; 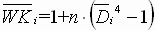 ; ; 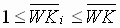 (1.14) (1.14)
Per-normal Natural Frequency (unitless):
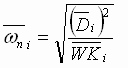 ; ;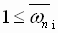 (1.15a) (1.15a)
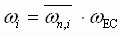 ; (1.15b) ; (1.15b)
Where wi is the application natural frequency in units consistent with wEC
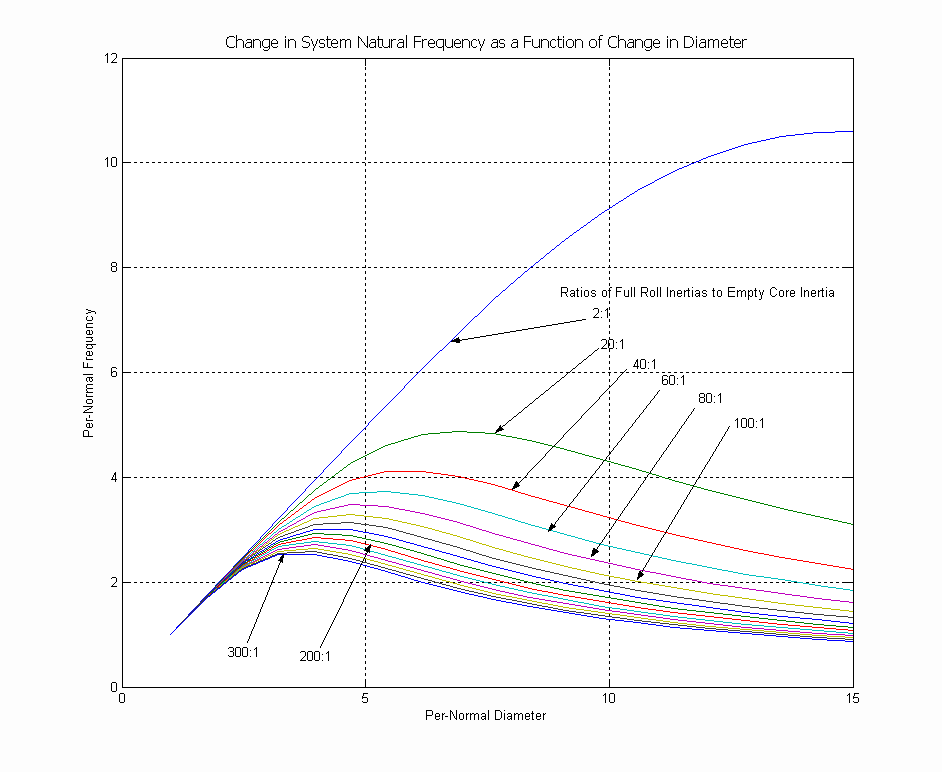
Figure 7b. Natural Frequency Vs Diameter (15:1 Diameter Ratio)
The following Figure 7c, shows how the shape of the natural frequency variation with diameter for a given set of inertia ratios, also varies with the diameter ratio.
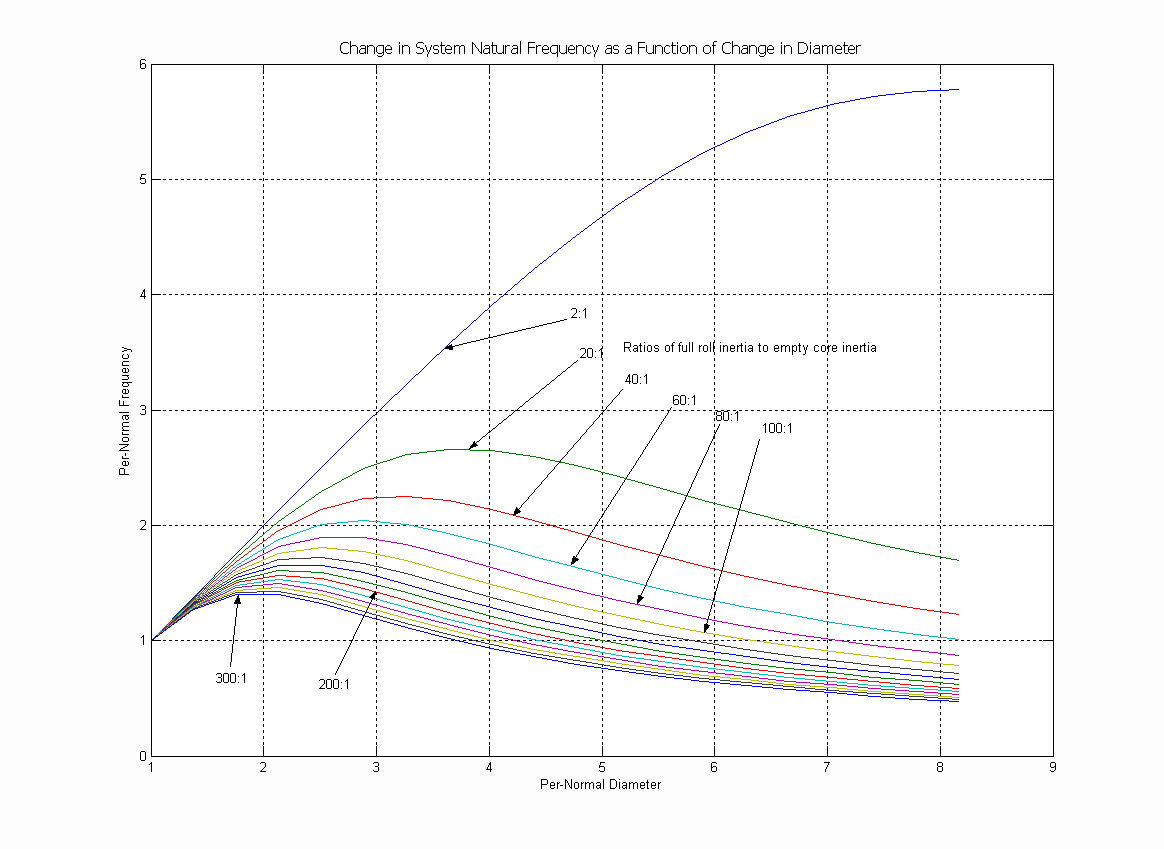
Figure 7c. Natural Frequency Vs Diameter (8:1 Diameter Ratio)
Estimating Full Roll Inertia
To obtain a reasonable estimate of the full roll inertia, the following equations can be used. Care must be taken to ensure that the correct units are used. Any input units that are not consistent with the indicated units must be converted to the shown units.
RFR = Full roll radius [in]
REC = Empty core roll radius [in] (includes core thickness)
d = Material density [lb / in^3]
W = Material width [in]
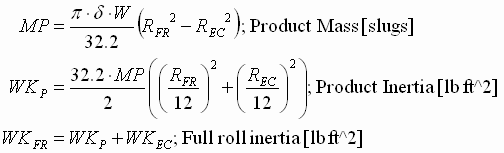 (1.16) (1.16)
The following table can be used for the product density:
|
Material |
Type |
[lb/in^3] |
|
Paper |
Hard |
0.035 |
| |
Kraft |
0.025 |
|
|
Polyethylene |
0.035 |
| |
Polypropylene |
0.032 |
|
Polystyrene |
|
0.037 |
|
Mylar |
|
0.036 |
|
Nylon |
|
0.036 |
|
Cellophane |
|
0.036 |
|
Teflon |
|
0.036 |
|
Aluminum |
|
0.097 |
|
Steel |
|
0.283 |
|
Brass |
|
0.305 |
|
Copper |
|
0.320 |
The empty core inertia (WKEC [lb ft^2]) can be approximated as twice the brake inertia. The brake inertia is available from the product data sheet. If gearing is used then the empty core inertia can be approximated as: 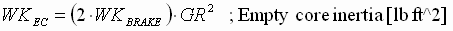
CHAPTER 2
SIMULATION STRUCTURE
Overview
The simulation is composed of two main sub-systems: The controller sub-system (yellow block) and the plant sub-system (blue block) as shown in Figure 9. Also included are references for line speed (magenta blocks) , wound-on tension, and tension reference (orange blocks). Scopes used for monitoring, and data storage blocks are represented by green blocks.
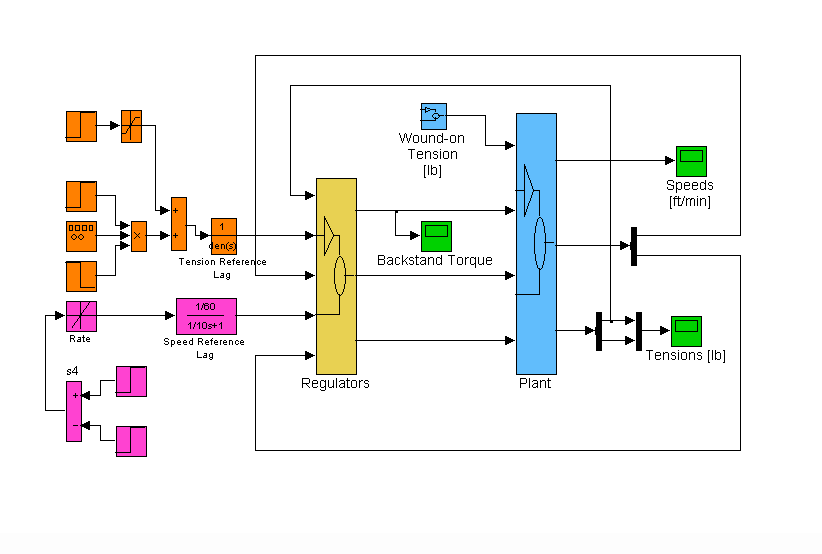
Figure 9. Simulation Main Block Diagram
Reference Generation
Two references are generated, a speed reference, and a tension reference. A winder wound-on tension reference can be used to investigate the effects of poor tension tapering in roll winding, for the investigation in this simulation it is set to zero. Following is a brief description of the speed and tension references.
Speed Reference
The speed reference (magenta blocks) is generated with a pure ramp that is lagged with a 10 [rad/sec] lag. The ramp acceleration and deceleration rates are set in units of [f.p.m. / sec]. Using an S-Curve for the speed reference provided a slight improvement in the tension error at the beginning and end of the line acceleration, however it was not significant.
Tension Reference
The default tension reference is set as a function of the user set PLI for the material used (default of 1 [PLI]): Tension [lb] = [PLI] x Width [in]. A small tension reference step train (orange blocks) was generated using a square wave generator. The magnitude of the steps was chosen such that the regulator torque reference did not saturate during the simulated run.
Plant sub-system
The plant sub-system is a block diagram of Eqís (1.1) through (1.11) in Chapter 1 and is shown in Figure 10. The web equations are masked in the green blocks, and the torque equations are masked in the light blue blocks. The web equations are coupled together with velocities, and the torque equations are coupled together with tensions as shown in Eqís (1.1) through (1.11).
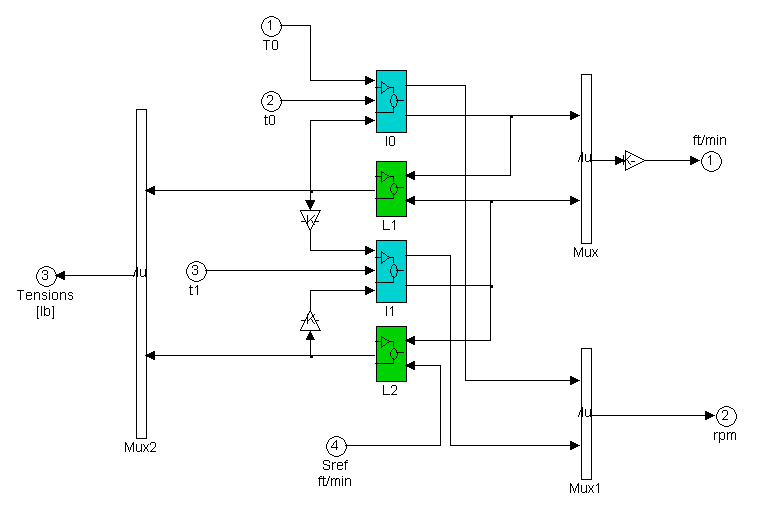
Figure 10. Plant Block Diagram
I0 Block Diagram
The I0 block diagram (Figure 11.) contains the torque equations describing the summation of torques in the backstand/winder system, and the change in diameter as a function of material thickness and rotational speed. (Eq's. 1.7-1.9).
The magenta blocks model the stiction phenomena that enables a backstand to produce a restraining torque. Briefly, the torque reference from the position controller can only produce a restraining torque when the roll is rotating. The magenta blocks that model this non-linear phenomena include magnitude limiting, rate limiting and square root gain blocks. Correctly setting these non-linear functions enables the simulation to closely mimic the non-linear friction behavior of a brake that is used to produce a restraining torque on a backstand. When simulating a clutch, the concept is the same except the torque is a motoring force and not a restraining force.
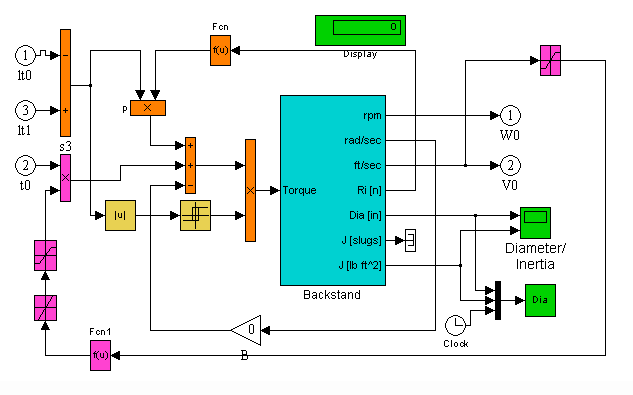
Figure 11. Backstand/Winder Block Diagram
The yellow blocks in Figure 11 model another friction phenomena known as static friction. Briefly, the differential load torque will not act on the system unless it exceeds a static friction value. This phenomena has a hysteresis characteristic that is modeled easily with a relay function. For more detailed explanations of these tribologic phenomena see [1], and [2].
Backstand Block Diagram
The backstand block is composed of the equations (1.5, 1.7 - 1.9) described in Chapter 1. It models the change in inertia as a function of roll diameter (magenta blocks). The roll diameter is modeled to vary as a function of rotational speed (yellow blocks). To simulate the effect of variations in roll diameter, the filtered rotational speed provides the once per rotation frequency for generating a sinusoidal disturbance to the roll diameter (cyan blocks). The torque divided by the Inertia [slugs] (orange blocks) is integrated to produce the roll rotational speed [rad/sec].
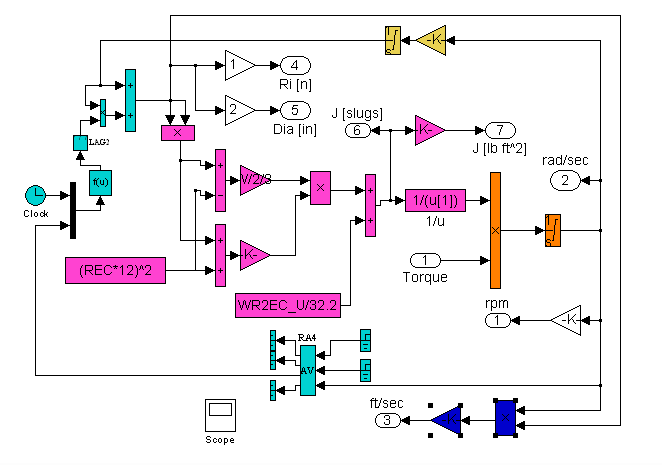
Figure 12. Backstand/Winder Block Diagram
L1 Block Diagram
L1 is a block diagram of Eq. (1.1). the blue blocks model the change in the T1 tension zone web length, as a function of tension Eq. (1.3). The magenta blocks represent the product of the non-linear E1 modulus of elasticity, and the cross sectional area. The dark blue block models the web material damping term Bw. The yellow blocks integrate the summed coupling velocities.
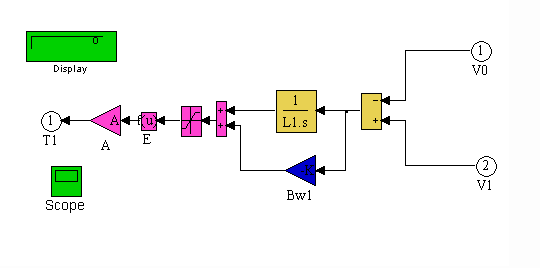
Figure 13. L1 Block Diagram
I1 Block Diagram
Figure 14. I1 block diagram models Eq. (1.5) for the cascaded torque regulated drive. No viscous damping was used in this section. The blue blocks integrate the summed torques acting on the roll inertia to produce a rotational speed [rad/sec]. The magenta blocks convert the rotational speed to a translational speed [ft/min].
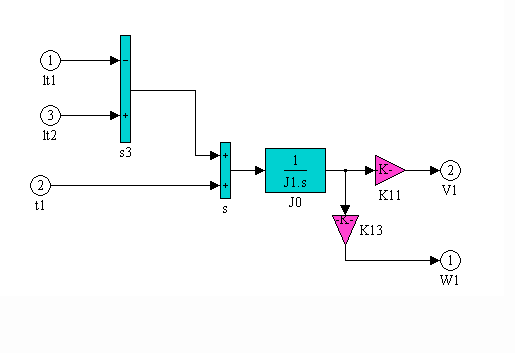
Figure 14. I1 Block Diagram
L2 Block Diagram
L2 is a block diagram of Eq (1.2). The magenta blocks represent the product of the non-linear E1 modulus of elasticity, and the cross sectional area. The dark blue block models the web material damping term Bw. The yellow blocks sum the coupling velocities and integrate them.
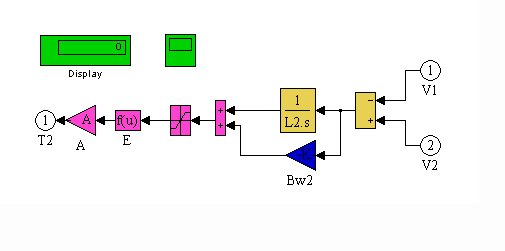
Figure 15. L2 Block Diagram
.
Regulators Sub-System
There are two controllers (Figure 16.) in the system. A cascaded torque controller for the drive that is used to isolate the ideal speed reference from the winder/backstand tension zone, and the non-linear adaptive tension regulator. Both of the controllers are modeled in the simulation with blocks that are implemented as discrete s-functions. The s-functions are written with difference equations and internal logic that exactly replicate the behavior of sampled digital control systems, including quantization errors.
The blue block represents the cascaded torque regulator, the yellow block represents the tension regulator. The second yellow block contains a model of the brake/clutch lag and transport delay.
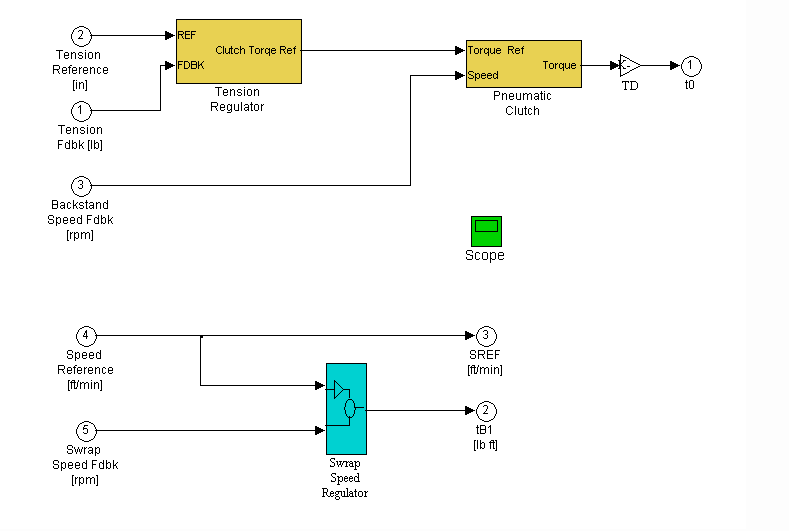
Figure 16. Regulators Block Diagram
Cascaded Torque Regulator Block Diagram
In order that the regulator be tuned in a per-normal manner (Figure 17) normalization (orange blocks) of the speed and torque references and feedbacks is used. The speed (cyan block) and torque (magenta blocks) regulators are tuned for a bandwidth of 5 [rad/sec]. The Torque reference is set to zero, therefore there is no tension difference between T1 and T2 when running at a constant line speed. Because there is no inertia compensation used in the torque regulator there is a small tension difference between T1 and T2 during acceleration and deceleration.
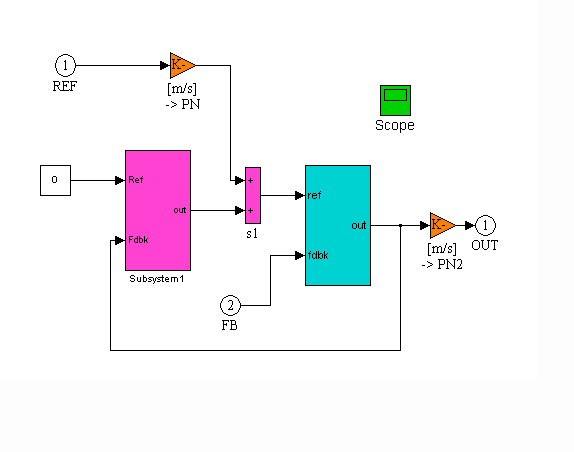
Figure 17. Cascaded Torque Regulator (CTR) Block Diagram
CTR Speed Regulator Block Diagram
The CTR speed loop block diagram is shown in Figure 18.
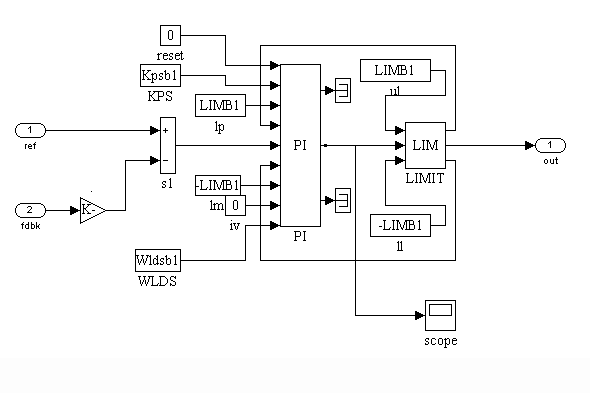
Figure 18. CTR Speed Regulator Block Diagram
CTR Torque Regulator Block Diagram
The CTR torque loop block diagram is shown in Figure 19.
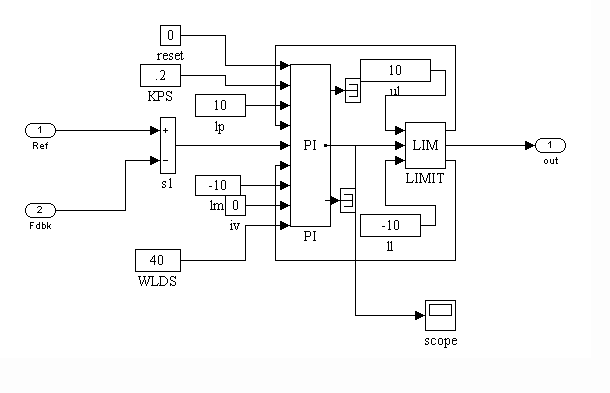
Figure 19. CTR Torque Regulator Block Diagram
>Tension Regulator Block Diagram
PROPRIETARY
CHAPTER 3
RESULTS
Overview
Two sets of simulation results are presented.
- The first set presents the results from simulations of unwinding with a backstand brake. These results show the efficacy of the gain and frequency 2nd order controller adaptation algorithms during a full wind-down of a roll from 50 [in] to approx. 3 [in].
- The second set presents results from simulations of winding with a clutch drive. These results show the efficacy of the gain and frequency 2nd order controller adaptation algorithms during a full windup of a roll from 3 [in] to approx. 50 [in].
For most of the results, the following plots are presented for each result set.
- Web Tensions [lb]
- Backstand/Winder torque [lb ft]
- Line speed [ft/min]
- Roll Diameter [in], and Inertia [lb ft2]
Other than those indicated by the plots, the parameters found in Appendix A were used during the simulation:
Unwinding, .003 [in], 0.025 [lb/in^3] W=12 [in], E=2.5e5, wEC=8 [rad/sec]

Figure 25. Web Tensions, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
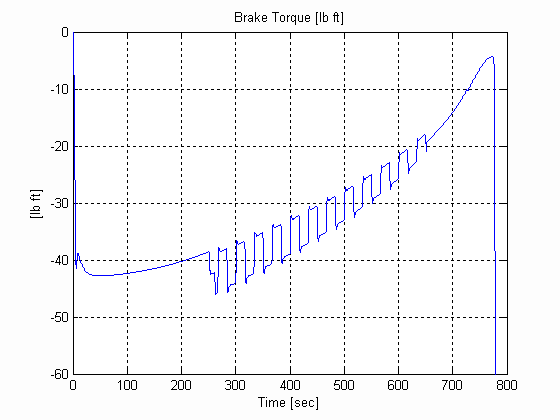
Figure 26. Backstand Torque, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
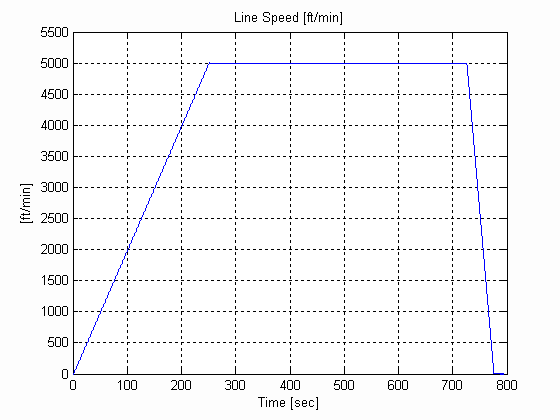
Figure 27. Line Speed, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
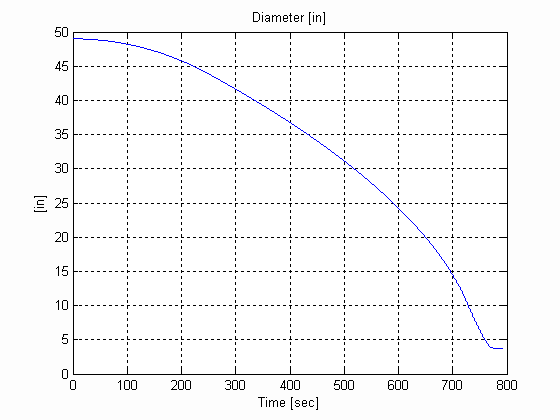
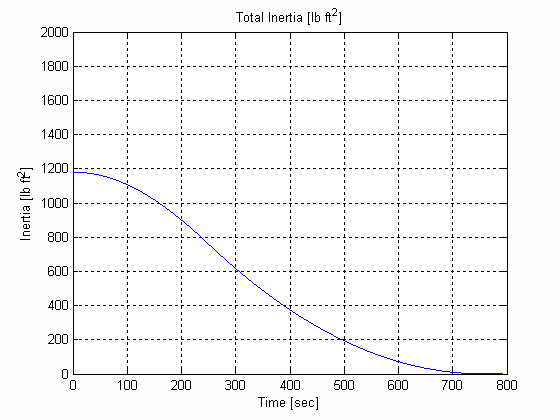
Figure 28. Diameter & Inertia, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
Unwinding, .003 [in], 0.025 [lb/in^3] W=12 [in], E=1.4e4, wEC=1 [rad/sec]
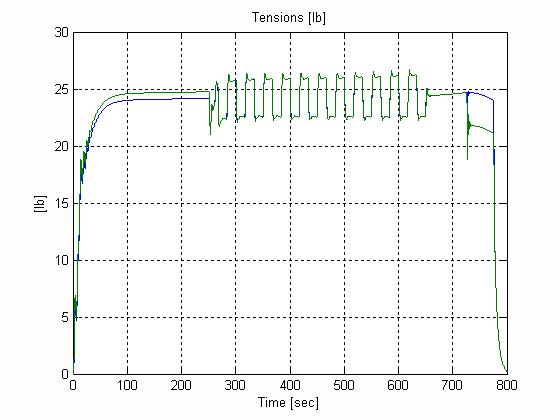
Figure 29. Web Tensions, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
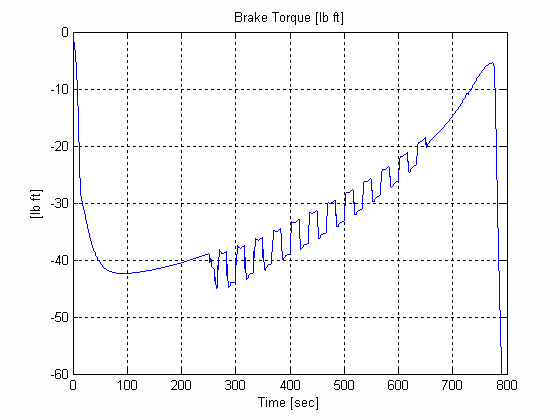
Figure 30. Backstand Torque, U, .003 [in], 0.025 [lb/in^3] W=12 [in]

Figure 31. Line Speed, U, .003 [in], 0.025 [lb/in^3] W=12 [in]


Figure 32. Diameter & Inertia, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
Unwinding, .003 [in], 0.025 [lb/in^3] W=6 [in], E=2.4e5, wEC=5 [rad/sec]
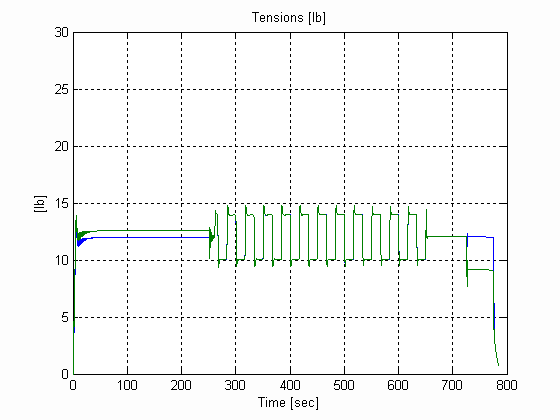
Figure 33. Web Tensions, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
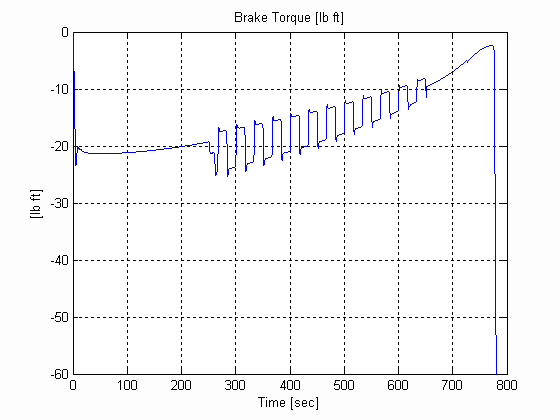
Figure 34. Backstand Torque, U, .003 [in], 0.025 [lb/in^3] W=12 [in]

Figure 35. Line Speed, U, .003 [in], 0.025 [lb/in^3] W=12 [in]


Figure 36. Diameter & Inertia, U, .003 [in], 0.025 [lb/in^3] W=12 [in]
Unwinding, .003 [in], 0.025 [lb/in^3] W=24 [in], E=1.4e4, wEC=2 [rad/sec]
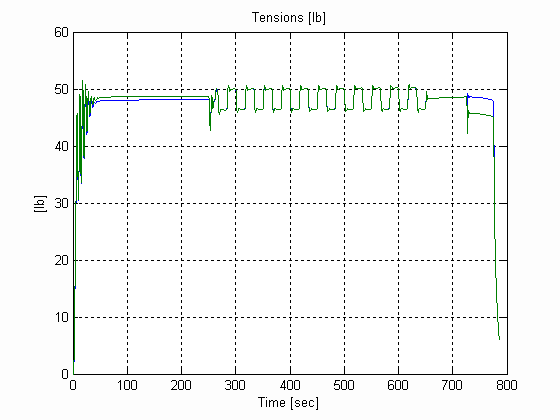
Figure 37. Web Tensions, U, .003 [in], 0.025 [lb/in^3] W=24 [in]
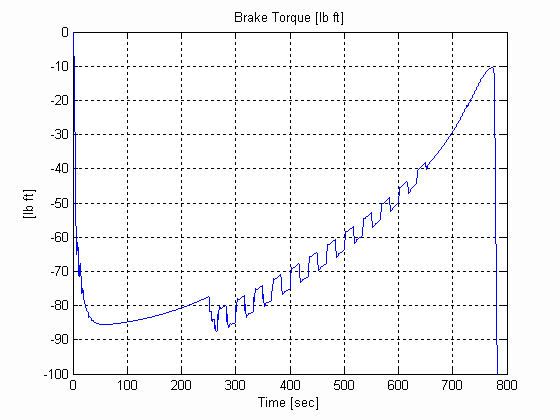
Figure 38. Backstand Torque, U, .003 [in], 0.025 [lb/in^3] W=24 [in]

Figure 39. Line Speed, U, .003 [in], 0.025 [lb/in^3] W=24 [in]


Figure 40. Diameter & Inertia, U, .003 [in], 0.025 [lb/in^3] W=24 [in]
Winding, .003 [in], 0.025 [lb/in^3] W=12 [in], E=2.5e5, wEC=5 [rad/sec]
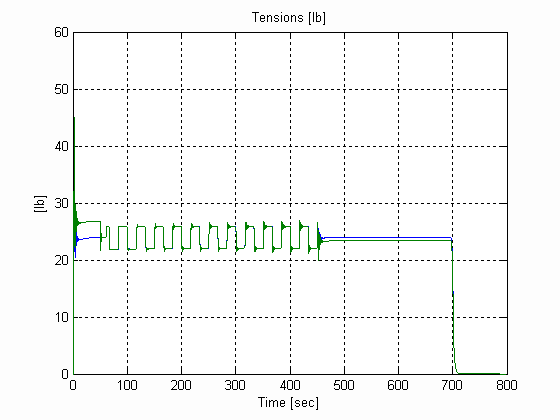
Figure 41. Web Tensions, W, .003 [in], 0.025 [lb/in^3] W=12 [in]
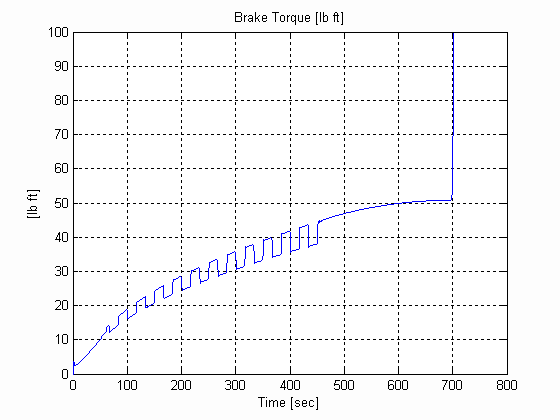
Figure 42. Winder Torque, W, .003 [in], 0.025 [lb/in^3] W=12 [in]
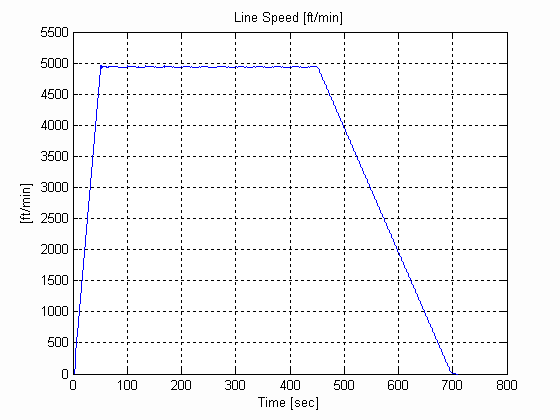
Figure 43. Line Speed, W, .003 [in], 0.025 [lb/in^3] W=12 [in]
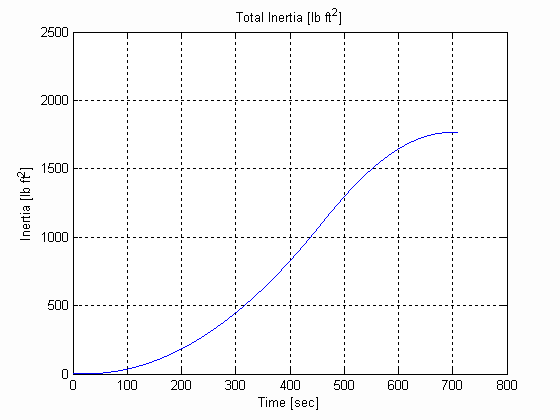
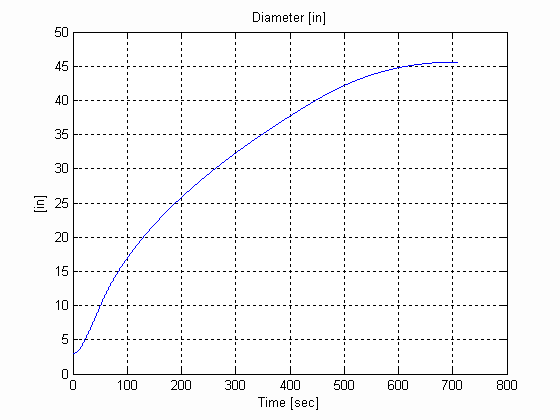
Figure 44. Diameter & Inertia, W, .003 [in], 0.025 [lb/in^3] W=12 [in]
Winding, .003 [in], 0.025 [lb/in^3] W=24 [in], E=1.4e4, wEC=2 [rad/sec]
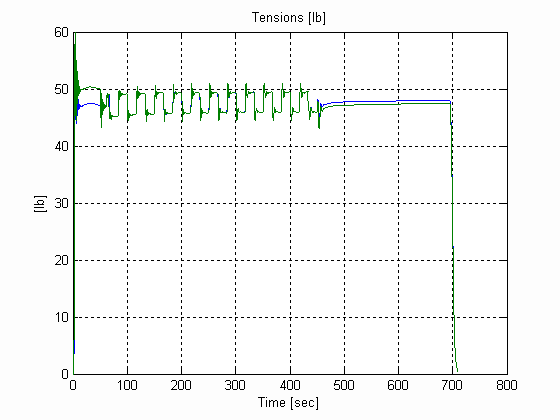
Figure 45. Web Tensions, W, .003 [in], 0.025 [lb/in^3] W=24 [in]
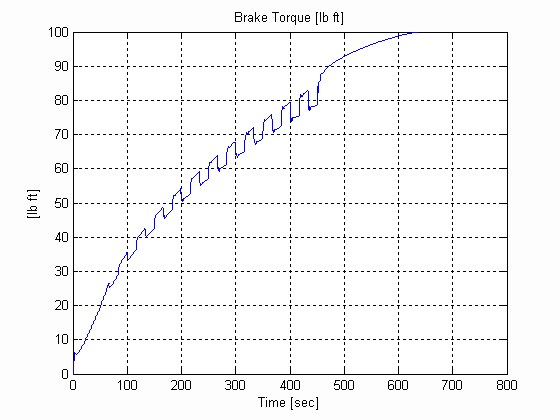
Figure 46. Winder Torque, W, .003 [in], 0.025 [lb/in^3] W=24 [in]

Figure 47. Line Speed, W, .003 [in], 0.025 [lb/in^3] W=24 [in]


Figure 48. Diameter & Inertia, W, .003 [in], 0.025 [lb/in^3] W=24 [in]
CHAPTER 4
SEQUENCING ISSUES & START-UP PROCEDURES
PROPROETARY
BIBLIOGRAPHY
[1] Hess, D.P., Soom, A. "Friction at a Lubricated Line Contact Operating at Oscillating Sliding Velocities" Journal of Tribology Transactions of the ASME Vol 112, pp 147-152, 1992.
[2] Majd, V.J.. Simaan M. A., "A Continuous Friction Model For Servo Systems With Stiction", Proceedings of the 4th I.E.E.E. Conference on Control Applications, Albany NY. 1996
|