FIELD SERVICE REPORT No. 42
|
To: |
(Proprietary) IP |
|
From: |
Brian Boulter ApICS LLC |
|
Date: |
January 13th 2001 |
|
Subject: |
Field Trip Report, International Paper, Erie PA. |
INTRODUCTION
At the request of the Erie PA. International Paper Plant Electrical Engineering department, the author made a field trip to address an instability problem in the unwinder dancer loop of an AUTOMAX DCS digital dancer control loop on a paper slitting machine. The drive used was a DPS DC drive connected to the DCS system with a fiber optic link. The instability was reported to occur when egg shaped rolls were processed through the machine. The instability was described as a growing oscillation in the dancer that peaked and eventually resulted in a web break at top speed and a 35 - 37.5" roll diameter. During machine accelerations and decelerations, the dancer was observed to be stable and responsive for rolls with uniform diameter, but showed poor control whenever a roll that had been in storage, and was consequently egg shaped, was loaded onto the Unwinder.
The dancer positioning loop as designed in the shipped DCS system had a fixed gain (both proportional and integral) dancer position PI regulator cascaded around a fixed gain (both proportional and integral) speed PI regulator. The speed feedback was taken from a resolver through a resolver card, and the dancer feedback was fed from a positioning potentiometer through an A/D card back into the DCS system. The configuration is shown in Fig. 1 below.
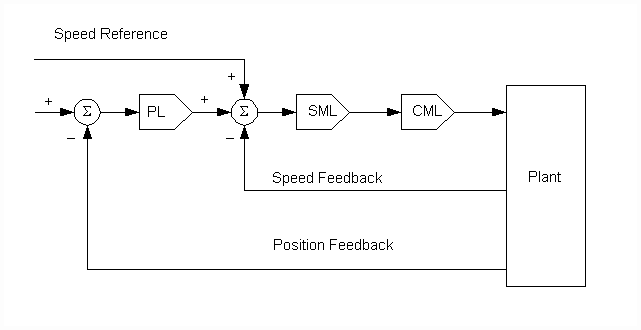
Fig. 1. Cascaded Position Loop Architecture.
The trip was made to the site on 1/13/01 – 1/16/01. The following observations and corrective actions were taken.
OBSERVATIONS:
Dancer Oscillations
While on-site the author observed the described instability, and noticed that it was line speed dependant, and roll diameter dependant. That is, at a lower line speed the instability occured at a smaller diameter than it did at top line speed (Top Line speed = 2500 [ft/min]). The following is a tabulation of the speeds and roll diameters at which the instability was observed
- At 500 [ft/min] NONE
- At 1000 [ft/min] NONE
- At 1500 [ft/min] SLIGHT @ Dia = 15 [in]
- At 2000 [ft/min] VERY BAD @ Dia = 27 [in]
- At 2500 [ft/min] WEB BREAK @ Dia = 36 [in]
Inertia Compensation
During acceleration and deceleration of the machine the author noted that the both the speed loop PI and the position loop PI integrator outputs climbed to about 25% rated output. This indicated that the inertia and friction compensation algorithms in the DCS dancer controller were not set-up correctly.
Loop Tuning
Both the speed and dancer position loops were fixed gain configurations. The build-up inertia variation in the winder was estimated with ApICS LLC's "Green-Sheet" program to be approximately 1500:1. The gear ratio of the Unwinder gear-box is 5.76:1 therefore the reflected inertia variation was estimated to be 45:1. This is a large variation in reflected inertia, and indicates a 45:1 variation in speed loop bandwidth over the roll build-up if a fixed gain regulator is used in the speed loop. Additional phase margin was required in the dancer position loop, especially at full roll. Both the structure and tuning of the dancer control loops was not adequate for this application.
The author verified that both the speed and position reference/feedback scaling was correct. The speed reference and the position loop trim to the speed loop were both correctly scaled as an inverse function of diameter.
CONCLUSIONS
The following conclusions were made based on the above observations:
- The unwinding zone natural frequency is a function of the inertia of the roll on the backstand (J1), the web modulus of elasticity (E), the web cross-sectional area (A), and the coupled inertia of the upstream sections (J2). The following explanation describes why these oscillations occur as a function of line speed V1, roll diameter (R1), and roll inertia , and what can be done to correct them. The natural frequency wf of a typical backstand system is given as
wf of:
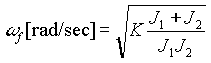 where: where: 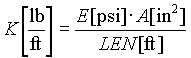 ; EQ. 0 ; EQ. 0
The inertia of each roll will vary with diameter as follows:
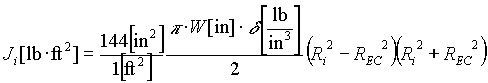 ; EQ. 1 ; EQ. 1
The general instantaneous winder/un-winder inertias are calculated using the instantaneous roll diameters:
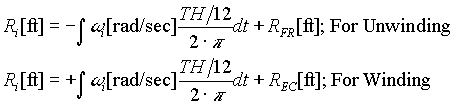 ; EQ. 2 ; EQ. 2
Where RFR is the initial condition full roll radius of the backstand roll, and REC is the initial condition empty core roll radius of the winder, and wi is the instantaneous roll rotational speed in units of [rad/sec].
The winder or unwinder roll surface speeds are calculated as a function of the motor rotational speed, the gear ratio, and the instantaneous roll radius:
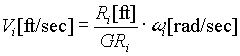 ; EQ. 3 ; EQ. 3
Equations 2 & 3 describe how the dominant second-order natural frequency of the approximate 2 mass - 1 spring system varies with roll diameter. The instantaneous value of the natural frequency will depend on the instantaneous value of the unwind roll. As the backstand unwinds, and feeds the slitter, its inertia J1 will decrease as the roll radius R1 decreases. The equation describing the decrease in the backstand roll radius is given by EQ. 2 (Unwinding). Substituting the instantaneous calculated values of J1 and J2 (from EQ 1 using the radii calculated in EQ. 2) into EQ. 0 will yield an approximation of the instantaneous dominant natural frequency of the line for that instant in time.
When imperfections exist in the roll on the backstand (usually an "egg-shaped" roll) a once-per-revolution (or occasionally a twice-per-revolution) disturbance will be introduced into the process. This disturbance can be heard as a noticeable audible "thump". The disturbance results from a rapid change in the exit speed of the web as it leaves the roll. The magnitude of these variations in roll surface exit speed (DVi) are proportional to the given line speed and the magnitude of the variation in roll diameter as shown in EQ. 4
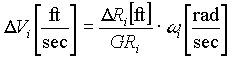 ; EQ. 4 ; EQ. 4
Where wi = the calculated motor speed for a given line speed and roll diameter.
The frequency wD of this disturbance will depend on the line speed and the roll diameter:
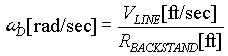 ; EQ. 5 ; EQ. 5
If the unwind roll is NOT fed into a dancer then a tension disturbance will result. For example, a system in which a tension regulated unwind feeds into a speed regulated bridle or calendar. The magnitude of the tension disturbance is then directly proportional to the elasticity of the material, and the change in roll surface described in EQ. 26. Frequency components of the disturbance that are outside the bandwidth of the tension regulator will pass directly into the process through the speed regulated bridle.
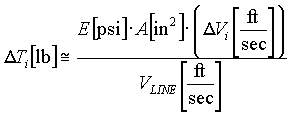 ; EQ. 6 ; EQ. 6
In this application, the small variations in surface speed, and the resulting tension deviations, will act on the dancer THROUGH the length of web attaching the dancer to the backstand. This is an important point to consider when we look at the effect of this disturbance on the system as a function of the natural frequency of the two inertia single spring system approximation described earlier.
Frequency components of the disturbance that are outside the bandwidth of the position regulator will not be compensated for by the position regulator, and, when this is the case, the dancer will be observed to oscillate at the same frequency as the disturbance (i.e. "in-sync" with the once-per-revolution disturbance of the backstand).
When the frequency of the disturbance wD (EQ. 5) coincides with the dominant second order natural frequency of the system wf (EQ. 0), the injection of energy into the closed system at the same frequency as the system natural frequency will stimulate the two inertias (i.e the backstand and the reflected upstream inertia) to exchange energy through the web that couples them together. Again, if the frequency components of the disturbance are outside the bandwidth of the position regulator they will not be compensated for by the position regulator, and consequently, the magnitude of the dancer oscillations will increase. The magnitude of the increase in the oscillations will depend on the elasticity of the material in the system. The more elastic, the greater the "stretch" of the material that will take place, and consequently the greater the movement of the dancer. The magnitude of the expected variation in dancer position is not easily quantified due to the non-linear stress-strain relationship associated with film and other plastic based materials.
To alleviate the problems associated with this phenomena when running the slitter, the operator can either slow down or speed up the machine when the oscillations occur, to ensure that the instantaneous disturbance frequency wD (or its second harmonic) does not coincide with the instantaneous system natural frequency at that instant in time. After 20 - 40 seconds, the desired line speed may be resumed.
The inertia compensation algorithm was not set up properly and needed adjustment A gain scheduled speed loop needed to be coded into the speed regulator. This is accomplished by scheduling the gain as a function of the calculated inertia. The speed loop gain must be limited to a maximum value that is slightly lower than the maximum gain the machinery is capable of withstanding before torsional resonance is excited in the drive train. The position regulator should be re-configured with feedback forcing to provide additional phase margin at full roll For extremely deformed rolls, the operator needed to be trained in identifying the excitation of the natural frequency, how to slow down the machine, and then how to accelerate the machine through the resonance once the diameter was adequately reduced at the lower line speed.
RECOMMENDATIONS
The oscillations observed in the dancer at certain line speeds and backstand roll diameters occurs when the frequency of the once-per-revolution backstand out-of-shape roll is coincident with the 2nd order dominant natural frequency of the system. To alleviate the problems associated with this phenomena when extremely egg-shaped rolls run through the machine, the operator should be trained to slow down or speed up the machine when the oscillations occur, to ensure that the once-per-revolution and natural frequencies are not co-incident.
- An Automatic speed reference control scheme could be implemented. This would automatically control the slow down and speed up of the machine when the natural frequencies approach co-incidence.
CORRECTIVE ACTIONS TAKEN:
- The Inertia compensation algorithm was adjusted such that the PI Loop Out on the speed regulator was within +/- 5% rated during line accelerations and decelerations.
- Friction compensation was not needed in this application.
- The ApICS LLC speed loop gain scheduling, and gain limiting stability equations were coded into the DCS speed controller.
- The ApICS LLC difference equations for a feedback forcing lead/lag compensator were coded into the dancer position loop.
- The Operator was instructed in recognizing the problem with egg-shaped rolls, and how to manipulate the machine speed reference to bypass the problem.
SUMMARY
After the above corrective actions were taken, the machine was run with stored stock for 3 hours without a web break. The operator was trained to recognize the instability and managed the machine such that no dancer instability was observed.
Feedback on the slitter's operation would be greatly appreciated.
|
